Множественная корреляция

При решении практических задач исследователи сталкиваются с тем, что корреляционные связи не ограничиваются связями между двумя признаками: результативным y и факторным x. В действительности результативный признак зависит от нескольких факторных. Например, инфляция тесно связана с динамикой потребительских цен, розничным товарооборотом, численностью безработных, объемами экспорта и импорта, курсом доллара, количеством денег в обращении, объемом промышленного производства и другими факторами.

В условиях действия множества факторов показатели парной корреляции оказываются условными и неточными. Количественно оценить влияние различных факторов на результат, определить форму и тесноту связи между результативным признаком y и факторными признаками x₁, x₂, …, x_k можно методами множественной (многофакторной) корреляции.

Математически задача сводится к нахождению аналитического выражения, наилучшим образом описывающего связь факторных признаков с результативным, т.е. к отысканию функции 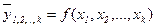. Выбрать форму связи довольно сложно. Эта задача на практике основывается на априорном теоретическом анализе изучаемого явления и подборе известных типов математических моделей. Среди многофакторных регрессионных моделей выделяют линейные (относительно независимых переменных) и нелинейные. Наиболее простыми для построения, анализа и экономической интерпретации являются многофакторные линейные модели, которые содержат независимые переменные только в первой степени:

,

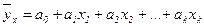где 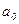– свободный член;

– коэффициенты регрессии;

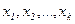– факторные признаки.

Если связь между результативным признаком и анализируемыми факторами нелинейна, то выбранная для ее описания нелинейная многофакторная модель (степенная, показательная и т.д.) может быть сведена к линейной путем линеаризации.

Параметры уравнения множественной регрессии, как и парной, рассчитываются методом наименьших квадратов, при этом решается система нормальных уравнений с (k+1) неизвестным:

где 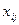– значение j-го факторного признака в i-м наблюдении;

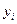– значение результативного признака в i-м наблюдении.

Как правило, прежде чем найти параметры уравнения множественной регрессии, определяют и анализируют парные коэффициенты корреляции. При этом систему нормальных уравнений можно видоизменить таким образом, чтобы при вычислении параметров регрессии использовать уже найденные парные коэффициенты корреляции. Для этого в уравнении регрессии заменим переменные y, x₁, x₂, …, x_k переменными t_j, полученными следующим образом:

, . ( ).

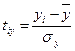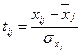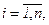
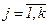Эта процедура называется стандартизацией переменных. В результате осуществляется переход от натурального масштаба переменных x_ij к центрированным и нормированным отклонениям t_ij. В стандартизированном масштабе среднее значение признака равно 0, а среднее квадратическое отклонение равно 1, т.е. 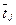=0, 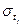=1. При переходе к стандартизированному масштабу переменных уравнение множественной регрессии принимает вид

,

где 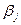( 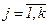) – коэффициенты регрессии.

Параметры уравнения множественной регрессии в натуральном масштабе и уравнения регрессии в стандартизированном виде взаимосвязаны:

( ).

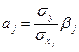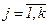Нетрудно заметить, что это обычная формула коэффициента регрессии, выраженного через линейный коэффициент корреляции.

Стандартизированные коэффициенты множественной регрессии 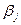также вычисляют методом наименьших квадратов, который приводит к системе нормальных уравнений

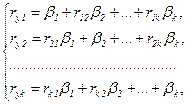
где – парный коэффициент корреляции результативного признака y с j-м факторным;

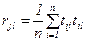– парный коэффициент корреляции j-го факторного признака с l-м факторным.

После того как получено уравнение множественной регрессии (в стандартизированном или натуральном масштабе), необходимо измерить тесноту связи между результативным признаком и факторными признаками. Для измерения степени совокупного влияния отобранных факторов на результативный признак рассчитывается совокупный коэффициент детерминации R² и совокупный коэффициент множественной корреляции R – общие показатели тесноты связи многих признаков независимо от формы связи. Приведем несколько формул для их расчета.

1. При линейной форме связи расчет совокупного коэффициента детерминации можно выполнить, используя парные коэффициенты корреляции:

,

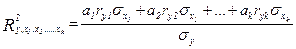где – параметры уравнения множественной регрессии в натуральном масштабе.

2. Еще легче вычислить совокупный коэффициент детерминации, используя уравнение регрессии в стандартизированном виде:

.

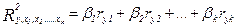3. Через соотношение факторной и общей дисперсий (или остаточной и общей дисперсий):

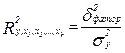, или ,

где 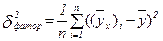– факторная дисперсия, характеризующая вариацию результативного признака, обусловленную вариацией включенных в анализ факторов; 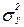– общая дисперсия результативного признака; 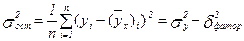– остаточная дисперсия, характеризующая отклонения фактических уровней результативного признака 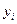от рассчитанных по уравнению множественной регрессии .

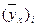Совокупный коэффициент множественной корреляции R представляет собой корень квадратный из совокупного коэффициента детерминации R². Пределы его изменения: 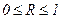. Чем ближе его значение к 1, тем точнее уравнение множественной линейной регрессии отражает реальную связь. Иначе говоря, среди отобранных факторов присутствуют те, которые решающим образом влияют на результативный. Малое значение R можно объяснить тем либо тем, что в уравнение множественной регрессии не включены существенно влияющие на результат факторы, либо тем, что установленная линейная форма зависимости не отражает реальной взаимосвязи признаков. Добиться адекватности модели множественной регрессии эмпирическим данным возможно, соответственно, либо включением в уравнение регрессии дополнительных, ранее не учитываемых факторов, либо построением нелинейной модели множественной регрессии.

Для более глубокого знакомства с темой «Множественная корреляция» необходимо воспользоваться литературой курса «Эконометрика».