Корреляция для нелинейной регрессии. Коэффициенты эластичности

Качество нелинейной регрессионной модели можно определить с помощью нелинейного показателя корреляции, который называется индексом корреляции для нелинейных форм связи R.

R можно вычислить на основе теоремы о разложении сумм квадратов. Сумма квадратов разностей между значениями результативной переменной и ее средним значением по выборке может быть представлена следующим образом:

,

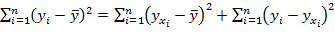где 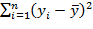- общая сумма квадратов (TSS – Total Sum Square); 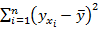- сумма квадратов объясненной регрессии (RSS – Regression Sum Square); 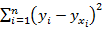- сумма квадратов остатков (ESS – Error Sum Square).

На основании данной теоремы

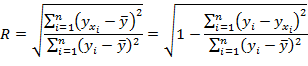
Индекс корреляции для нелинейных форм связи изменяется в пределах [0; 1] . Чем ближе его значение к единице, тем сильнее взаимосвязь между изучаемыми переменными.

Если возвести индекс корреляции в квадрат, то полученная величина будет называться индексом детерминации для нелинейных форм связи:

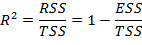
Индекс детерминации для нелинейных форм связи по характеристикам аналогичен обычному множественному коэффициенту детерминации. Индекс R² показывает, на сколько процентов построенная модель регрессии объясняет разброс значений зависимой переменной относительно среднего значения, т.е. какая доля общей дисперсии результативного признака объясняется вариацией факторных модельных признаков. Индекс детерминации можно назвать количественной характеристикой объясненной построенным уравнением регрессии дисперсии результативного признака. Чем больше значение данного показателя, тем лучше уравнение регрессии описывает выявленную взаимосвязь.

Кроме рассмотренных показателей, для изучения зависимости между результативной переменной и факторными признаками используются различные коэффициенты эластичности, которые позволяют оценить тесноту связи между переменными х и у.

Общий коэффициент эластичности показывает, на сколько процентов изменится результативный показатель у при изменении величины факторного признака на 1%. Формула расчета общего коэффициента эластичности имеет вид

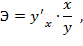
где 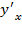- первая производная результативной переменной по факторному признаку.

Средний коэффициент эластичности вычисляется для среднего значения факторного признака 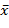по приведенной выше формуле:

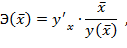
где 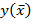- значение функции при среднем значении факторного признака.

Средний коэффициент эластичности характеризует процентное изменение результативного признака у относительно своего среднего значения при изменении факторного признака на 1% относительного 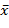. Такие коэффициенты рассчитываются по индивидуальным формулам для каждой разновидности функции.

Например, для показательной функции вида 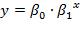средний коэффициент эластичности определяется как:

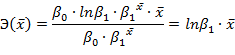
Основное достоинство степенной функции вида 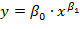заключается в том, что средний коэффициент эластичности равен коэффициенту регрессии:

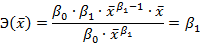
Помимо средних коэффициентов эластичности могут быть также рассчитаны точечные коэффициенты эластичности. Общая формула их расчета

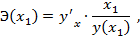
т.е. эластичность зависит от конкретного заданного значения факторного признака х₁.

Точечный коэффициент эластичности характеризует процентное изменение результативной переменной у относительно уровня функции у(х₁) при изменении факторного признака на 1% относительно заданного уровня х₁.

Например, для параболической функции 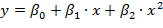точечный коэффициент эластичности находится следующим образом:

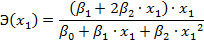
Знаменателем данного показателя является значение параболической функции в точке x₁.