Корреляция и корреляты

Корреляцией называется такая связь между переменными, когда по изменениям одной из этих переменных можно предсказывать изменения другой. В литературе по индустриально-организационной психологии распространенным примером такой связи является соотношение между возрастом и выраженной удовлетворенностью работой. За годы исследований во многих работах была обнаружена тенденция к положительной корреляции между этими переменными; это означает, что возрастание одной из них происходит вместе с возрастанием другой. С увеличением возраста в целом увеличивается и выраженная удовлетворенность работой. С другой стороны, между удовлетворенностью работой и отсутствием на работе часто обнаруживают отрицательную корреляцию; это значит, что с возрастанием одной из этих переменных другая убывает. С увеличением выраженной удовлетворенности работой уровень отсутствия на работе обычно падает.

Разработаны различные процедуры, с помощью которых можно определить, существует ли между двумя переменными, такими как возраст и удовлетворенность работой, корреляционная связь, а если существует, то положительная или отрицательная. Все эти процедуры основаны на одной и той же методике. Производится измерение обеих переменных у каждого испытуемого, и результаты измерений обрабатываются: помощью определенной вычислительной процедуры. Эта процедура позволяет получить коэффициент корреляции r, который уже упоминался выше.

В некоторых исследованиях одно из двух измерений, которые при корреляционном анализе проводят у каждого испытуемого, фактически является группой измерений. Индустриально-организационного психолога может, например, заинтересовать связь между результатами пяти отборочных тестов при приеме на работу и показателями учебы по программе профессиональной подготовки. Для исследования этой связи он может использовать процедуру множественной корреляции. Первое измерение — это измерение показателей подготовки каждого испытуемого. Второе измерение — это комбинированный результат тестирования (одно число), который математически выводится из результатов пяти различных отборочных тестов. Когда коэффициент корреляции для этих двух переменных рассчитан, результат обозначают через R (читается как «множественный R»), чтобы было ясно, что речь идет о большем числе переменных, чем обычные две.

Все коэффициенты корреляции, независимо от метода их расчета, лежат в диапазоне от -1,00 до +1,00. (В дальнейшем мы будем опускать знак «плюс» для положительных коэффициентов корреляции.) Значение коэффициента корреляции указывает на силу связи между переменными; чем оно ближе к 1,00 со знаком «плюс» или «минус», тем сильнее эта связь.

Коэффициент корреляции рассчитывается математически, но часто его представляют графически, в виде так называемого точечного графика. Вводится система координат с двумя осями, вдоль каждой из которых откладываются значения одной из переменных, и строятся точки, соответствующие результатам каждого испытуемого. На рис. 2.3 показан точечный график, отражающий относительные позиции 18 испытуемых по результатам грамматического теста и словарного теста. Один испытуемый (Испытуемый 5) получил по 60 баллов за оба теста. Большинство остальных испытуемых получили разные результаты за разные тесты, но явно существует сильная тенденция к тому, чтобы при высоком результате одного теста результат второго теста тоже был высоким.

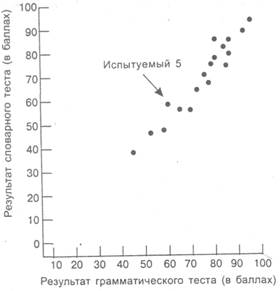
Рисунок 2.3. Точечный график, показывающий результаты (в баллах) грамматического теста и словарного теста

Рассчитанный по данным рис. 2.3 коэффициент корреляции r = 0,94. Из паттерна расположения точек, которые поднимаются из нижнего левого угла графика в верхний правый угол, видно, что это положительная корреляция. Если бы корреляция была отрицательной, то точки опускались бы из верхнего левого угла в нижний правый.