Вычисление поверхностного интеграла первого рода
1) Поверхность Φ, заданна параметрически
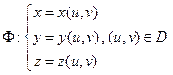
где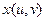 
, 
, 
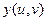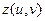− непрерывно дифференцируемые функции в их области определения D, r = (x, y, z) − радиус-вектор.
Для замкнутой области D − области определения функций х(u, v), y(u, v), z(u, v) − выберем некоторое разбиение ТD на частичные области Di, i = 1, ..., n. Каждой частичной области Di соответствует некоторая часть Фi поверхности Ф. Части Фi будем называть частичными областями поверхности Ф, а их совокупность T − разбиением поверхности Ф. Таким образом, любое разбиение поверхности определяется каким-либо разбиением области определения функций в правых частях параметрических уравнений.
В каждой частичной области Фi разбиения Т выберем произвольным образом точку Mi(xi, yi, zi). Предположим, что диаметр d(T) разбиения Т, т.е. максимальный из диаметров частичных областей, настолько мал, что проекция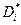 
частичной области Фi на касательную плоскость к поверхности Фi в точке Мi является взаимно однозначной, т.е. различные точки Фi имеют различные проекции на касательную плоскость.
Выберем некоторую частичную область Фi и зафиксируем. В точке Mi построим прямоугольную систему координат Miξηζ, соприкасающуюся с поверхностью (согласованную с поверхностью), т.е. такую систему координат, для которой плоскость ξMiη совпадает с касательной плоскостью к поверхности в точке Мi, а ось Miζнаправлена по нормали к поверхности. В окрестности точки Miповерхность Ф можно задать уравнениями
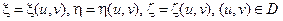(1)
Благодаря такому выбору системы координат Miξηζ, имеем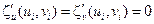 
, где ui и vi − значения параметров, соответствующие точке Мi. Плоская область 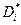расположена в координатной плоскости ξMiη, и ее площадь ΔSi можно подсчитать следующим образом:
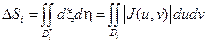
где J(u,v) − якобиан отображения (1) в точке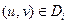 
. В последнем интеграле подынтегральную функцию |J(u, v)| заменим константой |J(ui, vi)|. Получим для площади ΔSi приближенное значение |J(ui, vi)|Δσi, где Δσi − площадь замкнутой области Di в плоскости переменных u и v. Погрешность δi этого приближения можно оценить следующим образом:
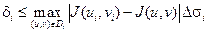
Суммируя по всем частичным областям получаем
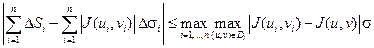
где σ − площадь замкнутой области D. При стремлении к нулю диаметра d(T)разбиения Т поверхности Ф к нулю стремится и диаметр d(TD)разбиения ТD замкнутой области D. При этом
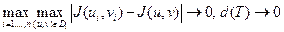
Для значения |J(ui, vi)| имеем
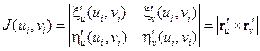
Нетрудно проверить, что
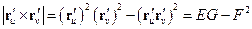
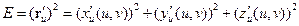
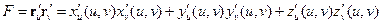
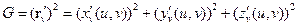
Тогда
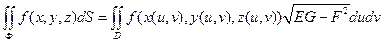
2) Поверхность Φ, заданна явно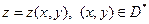 
(D* − проекция поверхности Φ на плоскость Oxy). Тогда
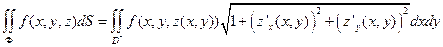
Геометрические и физические приложения поверхностного интеграла первого рода:
1) площадь поверхности;
2) масса материальной поверхности плотности μ: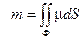 
3) координаты центра масс;
4) моменты инерции материальной поверхности относительно координатных плоскостей, осей координат, начала координат.
Дата добавления: 2015-10-13; просмотров: 636;