Общее решение задачи о колебании круглой мембраны
Вернемся к задаче о колебании круглой мембраны. С учетом того, что мы получили бесконечный набор значений λnm , полученные нами уравнения после применения метода разделения переменных следует переписать в следующем виде
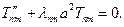 (24)
(24)
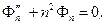 (25)
(25)
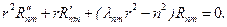 (26)
(26)
Решения этих уравнений соответственно будут иметь вид (после переобозначения произвольных констант)
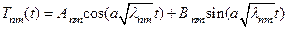 (27)
(27)
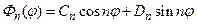 (28)
(28)
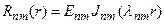 (29)
(29)
И тогда можем записать
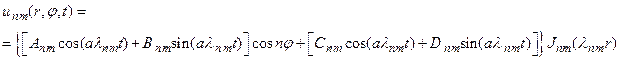
(30)
Здесь следует обратить внимание на то, константа стала не нужна. Следовательно, и вопрос об определении функции Jnm через неопределенный коэффициент a0 снимается с повестки дня. Общее решение уравнения колебания мембраны запишется как
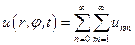 (31)
(31)
Для определения остальных констант воспользуемся начальными условиями
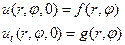 (32)
(32)
и ортогональностью функций Бесселя.
Подставив в общее решение 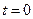 , получим
, получим
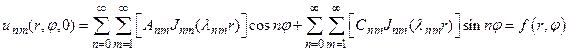 (33)
(33)
Этот ряд представляет собой разложение периодической функции 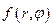 в ряд Фурье на интервале (0, 2π) и, следовательно, выражения в квадратных скобках должны быть коэффициентами рядя Фурье, а именно
в ряд Фурье на интервале (0, 2π) и, следовательно, выражения в квадратных скобках должны быть коэффициентами рядя Фурье, а именно
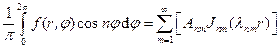 (34)
(34)
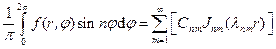 (35)
(35)
С другой стороны эти формулы представляют разложение функций в правых частях по функциям Бесселя. Тогда
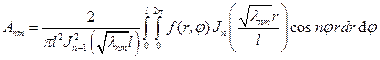 (36)
(36)
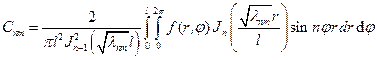 (37)
(37)
Аналогичным образом определяются и коэффициенты Bnm и Dnm после записи второго начального условия и подстановки в него производной по времени от общего решения. В результате в формуле (33) функция 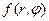 заменится на
заменится на 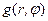 , коэффициенты Аnm и Сnm заменятся на Bnm и Dnm, а перед знаками суммирования появится множитель
, коэффициенты Аnm и Сnm заменятся на Bnm и Dnm, а перед знаками суммирования появится множитель 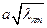 .
.
Дата добавления: 2015-10-13; просмотров: 814;
