Решение уравнения Бесселя.

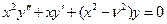
Будем искать решение уравнением Бесселя в виде обобщенного степенного ряда

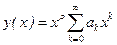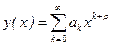или (14)

Чтобы определить коэффициенты ряда (14) нужно подставить его в уравнение (13) и собрать коэффициенты при одинаковых степенях х . После этого полученные коэффициенты при каждой степени х приравняем нулю, в результате получим

коэффициент при :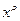

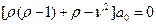
и если 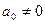, то будет следовать, что 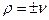. Положим сначала 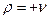, а потом окончательное решение запишем и для .

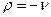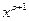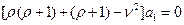Коэффициент при :

или

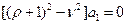, но вспоминая, что 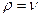, будем иметь

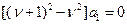
Поскольку 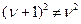, получаем, что .

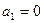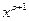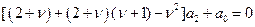Коэффициент при :

или

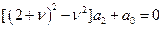, т.е.

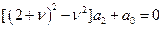
и в результате будем иметь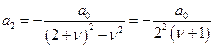

при этом a₀ остается не определенным (а значит, произвольным)

Имея выражение a₂ через a₀ можно предположить (и доказать), что и a_к будет выражаться через a_к-2 аналогичным образом , т. е.

( )

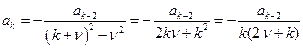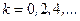В частности: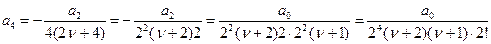

Тогда можно записать

( )

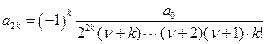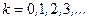Воспользуемся свойством гамма-функции

,

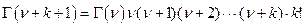но 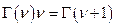и тогда

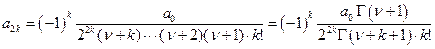
Если теперь выберем для произвольного a₀ выражение 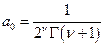, то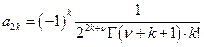

Тогда решение уравнения Бесселя можно записать в виде

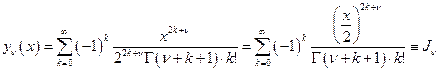функция Бесселя (15)

для :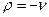

.

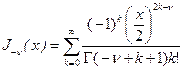Если ν – не целое число, то 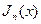и 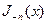являются линейными независимыми функциями, и из них можно составить общее решение уравнения. Если ν – целое, то можно показать, что .

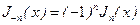В этом случае вводят в рассмотрение комбинацию из 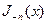и 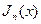следующего вида:

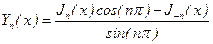, (16)

которая также является решением уравнения Бесселя и, кроме того, является линейно независимой функцией от .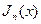

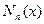называется функцией Неймана, которая тоже является специальной функцией.

При решении задачи о колебании мембраны у нас как раз 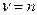– целое число и общее решение надо бы писать в виде

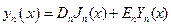
Однако, вспоминая граничное условие 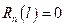и условие 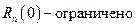, мы видим, что 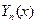в нуле неограниченно возрастает и, следовательно, надо положить .

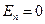Таким образом, общее решение имеет вид

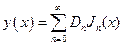(17)

Для определения значений λ воспользуемся граничным условием в виде

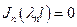(для каждого n) (18)

и получаем бесконечный набор трансцендентных уравнений, каждое из которых будет иметь бесконечное число решений (для каждого m), т.е. 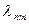, где m и n – целые числа. Тогда и функции Бесселя должны иметь двойную нумерацию J_{n m}.

график функции Бесселя.

график функции Неймана.

Если n – целое, то дробь в выражении (17) дает неопределенность типа 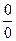, так как 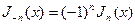. Следовательно будем рассматривать предел

.

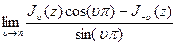Замечание: Функция Неймана нас интересовала только для целых n (так как в задаче круглой мембраны определялось, что n – целое), но сама по себе функция Неймана не обязательно содержит n в качестве целого числа.

Таким образом, функция Неймана в каждой точке z при n целом вычисляется как записанный выше предел.