Сети по опорным точкам

Вследствие неполного учета систематических ошибок снимка, вызываемых дисторсией объектива, атмосферной рефракцией и другими причинами, координаты точек сети, определенные по формулам (1.2.3) будут иметь систематические ошибки.

Систематические искажения сети маршрутной фототриангуляции можно описать с помощью полинома, например полинома 2-го порядка:

в которых:

Ai, Bi, Ci – коэффициенты полиномов,

X, Y, Z – координаты точек сети, определенные в результате внешнего ориентирования модели маршрута,

Xи, Yи, Zи – исправленные за влияние систематических ошибок координаты точек сети.

Для определения коэффициентов полиномов необходимо не менее чем 5 планово-высотных опорных точек, расположенных по схеме, представленной на рис. 1.2.5:

Y

X

O

Рис.1.2.5

так как каждая опорная точка позволяет составить 3 уравнения с 15 неизвестными коэффициентами полиномов Ai, Bi, Ci:

В уравнениях (1.2.4.2) Xи, Yи, Zи – геодезические координаты опорной точки в системе координат объекта.

В результате решения полученной системы уравнений (1.2.5) находят значения Ai,Bi,Ci. Если опорных точек больше 5, то решение производят по методу наименьших квадратов.

По координатам точек сети X,Y,Z и значениям коэффициентов Ai,Bi,Ci находят по формулам (1.2.4), исправленные за систематические искажения координаты точек сети Xи,Yи,Zи.

Следует отметить, что в случае если направление оси Xм системы координат модели маршрута не совпадает с осью X системы координат объекта (рис. 1.2.6), перед выполнением процесса исключения систематических ошибок необходимо предварительно перевычислить координаты X, Y, Z опорных и определенных в результате внешнего ориентирования модели

Y

Y^*

X^*

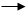
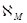
X

Рис. 1.2.6

маршрута точек во вспомогательную систему координат объекта OX^*Y^*Z^*, ось X^* которой параллельна оси Xм системы координат модели в системе координат объекта (рис. 1.2.6).

Затем производят устранение систематических искажений координат точек сети по методике описанной ранее в этом разделе, и перевычисляют
исправленные значения координат точек сети в систему координат объекта по формулам:

В формулах (1.2.6) и (1.2.7) матрицы преобразования координат 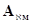и имеют вид:

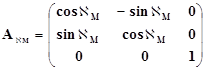и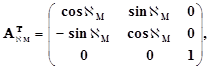

в которых: 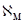- угол разворота системы координат модели.