Коэффициент вариации.

Вариация — это принятие единицами совокупности или группами различных, отичающихся друг от друга, значений знака. Вариация является результатом воздействия на единицу совокупности множества факторов. Синонимами терминация являются понятия изменение (изменчивость, вариативность’).

Вариация — одна из важнейших категорий статистической науки. Явления, подверженньие вариации, лежат в области исследования статистической науки, в то время как явления неизменные, статистические, постоянные в статистике не рассматриваются.

Практически все явления, имеющие естественный характер происхождения, подвержены изменчивости (например, химические процессы, , изменчивость наследственных признаков у каждого человека и др.). Явления, а также ряд естественных законов могут иметь неизменный характер (например, минимальный размер заработной платы)

Необходимо подчеркнуть значение исследования вариации в статистической науке:

1. Выявление измеычввости размеров явления дает возможность оценить степень зависимости изучаемого явления от других факторов, в свою очередь подверженньих изменчивости, или, другими словами, — оценить степень устойчивоти явленияк внешним воздействиям.

2. Вариация предполагает оценку однородности изучаемого явления, т. е. меру типичности, рассчитанной для этого явления средней величины.

Вариационным рядом называется последовательность различных вариант, записанных в возрастающем порядке вместе с соответствующими частотами.

В зависимости от типа признака различают дискретньие и интервальные вариационньие ряды. В зависимости от объема исходных данных и области допустимых значений одномерного количествснного признака, частотные распределения также подразделяются на дискретньие и интервальные. Если различных очень много (более 10—15), то эти варианты группируют вьибирая определенное число интервалов группировки и таким образом интервальное частотное распределение.

Первым шагом при построении интервального вариационого ряда является выбор определенного принципа, который дается в основу построения интервального ряда. Выбор этого принципа зависит от степени однородности рассматриваемой совокуности. Если совокупность однородна, то при построении ряда используют принцип равных интервалов. При этом вопрос однородности решается содержательным анализом изучаемых явлений.

Изменчивость явления в статистическом анализе отображается с помощью целого ряда характеристик, называемых системой показателей вариации. В нее входят:

абсолютные показатели вариации:

1) размах вариации;

2) средние величины (групповые и общие):

— степенные средние величины;

— структурные средние величины;

3) среднее линейное отклонение;

4) дисперсии (групповая, межгрулповая и общая) и среднее квадратическое отклонение;

относительные показатели вариации:

1) коэффициент осцилляции;

2) коэффициенты вариации (в том числе линейный);

3) коэффициенты детерминации (эмпирические и теоретические).

Размах вариации отражает пределы изменчивости признака или, другими словами, амплитуду вариации. Размах вариации рассчитывается как разность между максимальной величиной при знака (х) и минимальной величиной признака (х), т.е. по фор муле:

1.

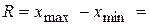
х — наибольшее значение признака;

х. — наименьшее значение признака.

Дисперсия — средний квадрат отклонений индивидуальньх значений признака от их средней величины:

Для вариационного ряда дисаерсия вычисляется по следующей формуле: (см. таблицу 2.)

Часто для исследования удобно представлять меру рассеяния в тех же единицах измерения, что и варианты. Тогда вместо дисперсии используют среднее квадратическое отклонение, которое является квадратным корнем из дисперсии, т.е. среднее квадратичное отклонение вычисляется по формуле: (см. таблицу 2)

Рассмотренные выше меры рассеявия (размах вариации, дисперсия, среднее квадратическое отклонение) являются абсолютными величинами, судить по ним о степени колеблимости признака не всегда возможно, в некоторых задачах необходимо использовать относительные показатели рассеяния. Таким показателем является коэффициент вариации (V), который представляет собой отношение среднего квадратичного отклонения к средней арифметической, выраженное в процентах:

Коэффициент вариации позволяет:

— сравнивать вариацию одного и того же признака у разных групп объектов;

— выявить степень различия одного и того же признака одной и той же группы объектов в разное время;

— сопоставить вариацию разных признаков у одних и тех групп объектов.

Если значение коэффициента вариации не превышает 33 то изучаемая совокупность считается однородной.

Рассмотрим на примере методику расчёта среднего квадратического отклонения и дисперсии признака.

ПРИМЕР 5 . В результате выборочной проверки расфасовки чая получены следующие данные:

Масса пачки чая, г. Число пачек чая , шт.

До 49 г. 17

49-50 52

50-51 21

51-52 7

52 и выше 3

ИТОГО : 100

Исчислить среднюю массу пачки чая,среднее квадратическое отклонение,дисперсию признака.

Для расчёта используем формулы из таблицы 2.

Все расчёты желательно оформить в виде таблицы. Для определения середины интервала

В каждой группе ,т.е. среднего значения,необходимо от интервального перейти к дискретному ряду. Величина интервала равна 1 (например,50 – 49 =1 ).Значит среднее значение для первой группы составит ( (48 +49) /2 = 48,5 ;для второй и третьей групп соответственно 49,5 и 50,5 и т. д.

Масса Число Середина Х*f Х – Х ( Х – Х ) ( Х – Х ) * f