Взаимосвязь индексов.
Индекс (от лат.— показатель,) — статистический относительньий показатель, характеризующий соотноше социально-экономических явлений во времени, в пространстcтве или выборе в качестве базы сравнения какого-либо условно уровня. С помощью индексов можно определить количественные изменения самых различных показателей функционирования народного хозяйства, развития социально-экономических процессов и т.п.
В экономической работе с помощью индексов можно объективно и точно показать изменения в росте или снижении производства, изменения в урожайности, состоянии себестоимости цен выпускаемой продукции, численности работающих, производительности труда, заработной платы, изменения цен на фондовых рынках и прочие.
От средних величин индексы отличаются тем, что они воплощают в себе, как правило, сводные, обобщающие показатели т.е. выражают некоторое содержание, свойственное всем рассматриваемым явлениям и процессам. Например, предприятие, выпускающее многообразную продукцию, нельзя оценить путем сравнения изменения объемов производства с помощью простого сложения единиц выпускаемой продукции, необходим какой- то общий измеритель. Таким измерителем становится стоимость или себестоимость.
При всем разнообразии индексы можно подразделить на две группы. Одни показатели выражаются абсолютными величинами, свойственными всем единицам статистической совокупности, другие представляют собой показатели, рассчитанные на ка кую-то единицу (показатели цен, себестоимости, урожайности, производительности труда, заработной платы и т.п.). Условно первая группа показателей называется количественными, и вторая группа условно называетсякачественными показателями. Наиболее типичным индексом количественного показателя является индекс объема, т.е. индекс физического объема продукции , товарооборота, национального дохода и др.
Индексы качественных показателей--- это индексы цен, себестоимости, издержек обращения,покупательной способности рубля,производительности труда и др.
С точки зрения охвата элементов различают ---индексы индивидуальные и общие.
Индивидуальные индексы обозначаются (i ) и характеризуют динамику отдельных элементов, входящих в совокупность.
В зависимости от методики расчета общие индексы (I ) подразделяются на:
-- агрегатные;
-- средние из индивидуальных ( средние арифметические и средние гармонические)
На примере т/оборота рассмотрим все перечисленные индексы:
Введём условные обозначения : p – цена, q – физический объём т/оборота, или количество реализованных товаров. Произведение цены ( p) и количества реализованных товаров( q)
Даёт т/оборот : p * q = pq.
Индивидуальные индексы являются однотоварными , т.к. характеризуют изменение цены или физической массы одного товара в отчётном периоде по сравнению с базисным,
Индивидуальный индекс цен обозначается ( ip ) и рассчитывается по формуле:ip = p1 / p0
где / p0—цена в базисном периоде;
p1 –цена в отчётном периоде.
Если по условию задачи дано изменение цен в %, тогда ipопределяется по формуле:
ip = 100 + изменение цен в %
Пример 1. Рассчитать индивидуальные индексы по каждому товару. Для расчета используем формулу :ip = p1 / p0
Где цена в январе – это цена в базисном периоде, а цена в сентябре – это цена в отчётном периоде.
| Наименование товара | Цена за 1кг. в янв. | Цена за 1кг.в сент. | i | |
| Яблоки | 37.50 | 38.2 | 1.019 | |
| Киви | 62.8 | 64.3 | 1.024 | |
| Апельсины | 26.6 | 25.9 | 0.974 | |
| Лимоны | 34.7 | 34.5 | 0.994 | |
| Мандарины | 49.4 | 50.8 | 1.028 |
Например: индивидуальный индекс цены по яблокам составит: 38,2 : 37,5= 1,019,что означает цена за 1 кг. Яблок в сентябре увеличилась посравнению с январём на1,9%
(значение индекса 1,019 выразили в % 1,019х100%=101,9%, 101,9% - 100%=+1,9% ).
Индивидуальный индекс физического объёма т/оьорота обозначается iq и рассчитывается по формуле:
i = q1 / q0 где q0 --- физический объём товара в базисном периоде;
q1---- физический объём того же товара в отчётном периоде.
Общие индексы являются многотоварными т.к. определяют изменение цен или физического объёма товарной массы всех или нескольких товаров. Агрегатные индексы выступают как основная форма общего индекса ,а средние индексыполучают путём преобразования агрегатных. (см. таблицу 5.)
В экономических категориях существует зависимость: цена, умноженная на физический объём товарной массы, даёт т/оборот (p х q= pq). Такая же взаимосвязь существует и в индексах: индекс цен, умноженный на индекс физического объёма , даёт индекс т/оборота: Ip х Iq = Ipq
Если вместо обозначенных 2-х первых индексов запишем агрегатные индексы цен и физического объёматоварной массы , то получим индекс товарооборота в фактических ценах , который покажет изменение т/оьорота за счёт двух факторов ,(цен , и количества).
(см. таблицу 5.) Взаимосвязь индексов показана в таблице 6.
ПРИМЕР 2.На основании данных о реализации товаров в магазине вычислить:
1)индивидуальные индексы цен покаждому товару;
2)СРЕДНИЙ ГАРМОНИЧЕСКИЙ индекс цен;
3)СРЕНИЙ АРИФМЕТИЧЕСКИЙ индекс физического объёма т/оьорота;
4)ОБЩИЙ ИНДЕКС Т/ОБОРОТА в фактических ценах;
5)Выявите взаимосвязь индексов в относительном и абсолютном выражении.
Для определения индивидуальных индексов используем формулу:
ip = 100 + изменение цен в %
Тогда ,например ipпо товару А , ip = 100 +5 = 1,05 ,и т.д.
Для расчета средних индексов воспользуемся формулами из таблицы 5
| Товары | Реализация в т.р. | Изменение цен в % | I | pq/i | |
| Баз. Пер. | Отч.пер. | ||||
| А | 480.5 | +5 | 1.050 | 457.6 | |
| Б | 680.7 | 690.9 | +10.5 | 1.105 | 625.2 |
| В | 215.6 | 250.8 | 1.000 | 250.8 | |
| Итого: | 1306.3 | 1422.2 | 1333.7 | ||
| Средний гармонический индекс цены | 1.066 | 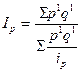
| 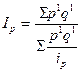
| ||
| Средний арифметический индекс физ. Объёма т/о | 1.021 | ||||
| Формула компонентной связи общих индексов | 1.089 | ||||
| Общий индекс т/о | 1.089 |
Вывод: т/оборот в отчётном периоде по сравнению с базисным возрос на 8,9% , в т.ч. за счёт изменения цен на товары , т/оборот увеличился на 6,6% , а за счёт изменения физической массы возрос на 2,1%.
Абсолютный прирост т/оборота за счёт изменения цен : (1422,2 – 1333,7 =+ 88,5 т.р.),за счёт изменения физической массы : ( 1333,7 – 1306,3 = +27,4 т.р.).
Абсолютный прирост т/оборота засчёт 2-х факторов = ( 1422,2 – 1306,3 =115,9 т.р.)
Взаимосвязь индексов в относительном выражении:
Ip х Iq = Ipq , подставим в эту формулу значения: 1,089 = 1,066 х 1,021
Взаимосвязь в абсолютном выражении:
Δåpq ( p q) = Δåpq (p) + Δåpq (q)
Подставим значения:
115,9т.р. = 88,5т.р. + 27,4т.р
Дата добавления: 2015-10-09; просмотров: 3467;
