Теоретическое введение. Колебательным контуром называется электрическая цепь, состоящая из включенных последовательно катушки индуктивностью L
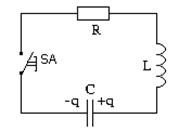 Рис. 20.1 Рис. 20.1
|
Колебательным контуром называется электрическая цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R (рис. 20.1).
Колебательные контуры служат для возбуждения и поддержания электромагнитных колебаний. Если в колебательном контуре отсутствуют внешние источники электрической энергии, то для возбуждения в контуре колебаний необходимо предварительно зарядить конденсатор. По второму правилу Кирхгофа для контура на рис.20.1 можем записать:
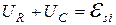 , (20.1)
, (20.1)
где 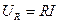 – напряжение на активном сопротивлении,
– напряжение на активном сопротивлении, 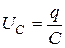 – напряжение на конденсаторе,
– напряжение на конденсаторе, 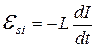 – ЭДС самоиндукции, возникающая в катушке индуктивности. Тогда из (20.1) получим:
– ЭДС самоиндукции, возникающая в катушке индуктивности. Тогда из (20.1) получим:
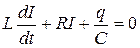 . (20.2)
. (20.2)
Далее учтем, что сила тока в цепи – это производная заряда конденсатора по времени: 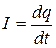 , а
, а 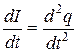 , тогда после почленного деления уравнения (20.1) на L получим:
, тогда после почленного деления уравнения (20.1) на L получим:
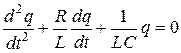 . (20.3)
. (20.3)
Уравнение (20.3) представляет собой дифференциальное уравнение свободных затухающих колебаний, амплитуда которых уменьшается с течением времени вследствие потери энергии на джоулево тепло в резисторе R.
Если ввести в рассмотрение коэффициент затухания b=R/2L и собственную частоту колебаний w0 (w02=1/(LC)), представляющую собой частоту гармонических колебаний в идеальном колебательном контуре (при R=0):
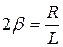 ;
; 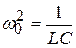 , (20.4)
, (20.4)
то уравнение (20.3) можно записать в виде:
 . (20.5)
. (20.5)
При этом колебания заряда будут совершаться по закону:
 , (20.6)
, (20.6)
где циклическая частота затухающих колебаний ω меньше частоты собственных гармонических колебаний w0:
 , (20.7)
, (20.7)
а амплитуда с течением времени уменьшается по экспоненте:
A(t)=q0e-βt. (20.8)
Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими. Если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами заряда и определять по формуле:
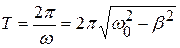 (20.9)
(20.9)
Одной из величин, характеризующих быстроту затухания колебаний, является логарифмический декремент затухания l, численно равный натуральному логарифму отношения амплитуд двух следующих друг за другом колебаний:
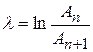 , (20.10)
, (20.10)
где колебания с номерами n и (n+1) отстоят друг от друга по времени на один период:
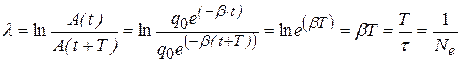 . (20.10а)
. (20.10а)
Здесь А(t) – амплитуда заряда на обкладках конденсатора в момент времени t; А(t+T) – амплитуда заряда в момент времени (t+T); t - время релаксации, то есть промежуток времени, в течение которого амплитуда колебаний уменьшается в e раз (е – основание натурального логарифма); Ne- число колебаний, совершаемых за время t.
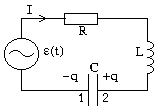 Рис. 20.2
Рис. 20.2
|
Логарифмический декремент затухания связан с добротностью контура Q, которая при малых значениях l равна:
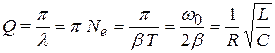 . (20.11)
. (20.11)
Чтобы в реальном колебательном контуре (рис.20.2) получить незатухающие электромагнитные колебания, в него нужно включить источник электрической энергии, ЭДС e которого изменяется с течением времени по гармоническому закону:
e(t)=e0cos(w. t). (20.12)
В колебательном контуре устанавливаются вынужденные колебания с частотой w. Эти колебания можно рассматривать как протекание в цепи, содержащей резистор сопротивлением R, катушку индуктивностью L и конденсатор емкостью С, переменного тока, который можно считать квазистационарным. Величину тока I определим, записав второе правило Кирхгофа для замкнутого контура:
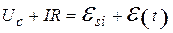 , (20.13)
, (20.13)
где ЭДС самоиндукции равна
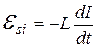 , (20.14)
, (20.14)
а напряжение на конденсаторе
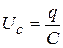 . (20.15)
. (20.15)
Поскольку сила тока
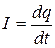 , (20.16)
, (20.16)
то после подстановки в (20.13) выражений (20.14) – (20.16) и деления на L получим:
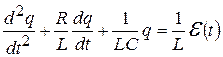 . (20.17)
. (20.17)
Использовав понятие коэффициента затухания b и частоты свободных незатухающих колебаний w0, уравнение (20.17) можно преобразовать к виду:
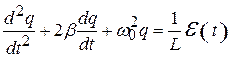 , (20.18)
, (20.18)
Если e(t) меняется с течением времени по гармоническому закону (20.12), решением уравнения (20.18) будет гармоническая функция:
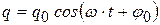 (20.19)
(20.19)
с амплитудой q0 и начальной фазой j0, зависящими от частоты w:
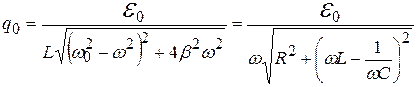 , (20.20)
, (20.20)
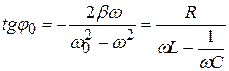 . (20.21)
. (20.21)
Силу тока в колебательном контуре при установившихся вынужденных колебаниях в нем найдем из (20.19):
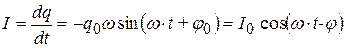 , (20.22)
, (20.22)
где
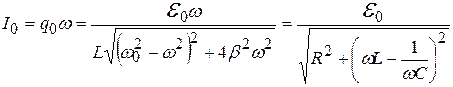 , (20.23)
, (20.23)
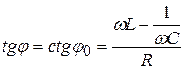 . (20.24)
. (20.24)
Зависимость I0(w) не является монотонной функцией w, а достигает максимального значения при
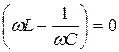 . (20.25)
. (20.25)
Значение w,при которой I0 имеет максимальное значение, называется резонансной частотой wрез. Из (20.25) следует, что
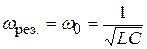 . (20.26)
. (20.26)
Явление резкого возрастания амплитуды вынужденных электромагнитных колебаний при приближении частоты питающей ЭДС к частоте собственных колебаний контура называется электрическим резонансом.
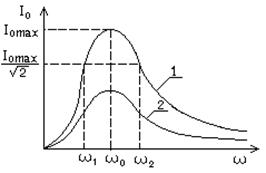 Рис. 20.3
Рис. 20.3
|
Графики зависимости I0(w) при различных сопротивлениях цепи R называются резонансными кривыми колебательного контура (рис.20.3).
Найдем падение напряжения на отдельных участках показанной на рис. 20.2 цепи переменного синусоидального тока, определяемого соотношением (20.22):
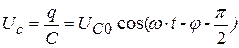 , (20.27)
, (20.27)
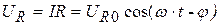 , (20.28)
, (20.28)
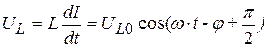 , (20.29)
, (20.29)
причем
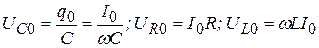 , (20.30)
, (20.30)
или
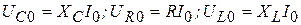 , (20.31)
, (20.31)
где 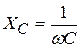 – емкостное сопротивление,
– емкостное сопротивление, 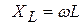 – индуктивное сопротивление, R –активное электрическое сопротивление.
– индуктивное сопротивление, R –активное электрическое сопротивление.
Величина 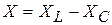 называется реактивным сопротивлением электрической цепи, а
называется реактивным сопротивлением электрической цепи, а
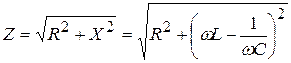 (20.32)
(20.32)
полным сопротивлением, или импедансом. Пользуясь этими понятиями, можно записать:
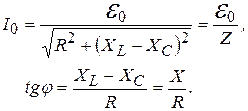 (20.33)
(20.33)
При 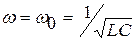 из (20.32) и (20.33) получим:
из (20.32) и (20.33) получим: 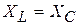 , тогда
, тогда 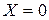 , а полное сопротивление Z принимает минимальное значение
, а полное сопротивление Z принимает минимальное значение 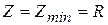 . В этом случае
. В этом случае
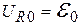 ,
,
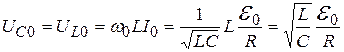 , (20.34)
, (20.34)
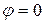 .
.
Так как UC и UL согласно (20.27) и (20.29) изменяются в противофазе, а амплитуды их одинаковы (20.34), то общее падение напряжения на участке цепи 1-R-L-2 (рис.20.2)
U=UR+UL+UC=UR=e0cos(wt). (20.25)
Рассмотренный случай резонанса называют резонансом напряжений. Нетрудно видеть из (20.34), что при резонансе напряжений
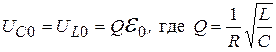 . (20.26)
. (20.26)
На рис. 20.4 приведены зависимости амплитудного значения напряжения на конденсаторе (кривая 1) и напряжения на выходе генератора (кривая 2) от частоты питающей ЭДС. Из приведенных зависимостей видно, что наибольшее значение амплитуда напряжения на конденсаторе имеет при w < w0.
 Учитывая, что
Учитывая, что 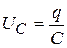 и q изменяется в соответствии с (20.20), можно показать, что частота, при которой максимально напряжение на ёмкости
и q изменяется в соответствии с (20.20), можно показать, что частота, при которой максимально напряжение на ёмкости
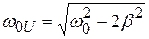 . (20.27)
. (20.27)
Вид резонансных кривых колебательного контура для различных значений R представлен на рис. 20.3. 1 – резонансная кривая для контура с меньшим сопротивлением, чем кривая 2:
R1< R2,
тогда в соответствии с (20.26) добротности контуров: Q1 > Q2. "Остроту" резонансных кривых можно охарактеризовать с помощью относительной ширины Dw/w, где Dw – разность значений w2 и w1 циклических частот, соответствующих значению тока (рис.20.3):
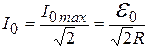 .
.
Из (20.23) получим уравнение для w1 и w2:
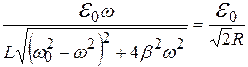 ,
,
имеющее 4 корня – два отрицательных и два положительных. Поскольку частота должна быть w>0, то оставим только положительные корни:
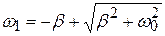 ;
; 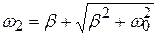 , (20.28)
, (20.28)
тогда Dw=w2–w1=2b. Следовательно, относительная ширина резонансной кривой колебательного контура равна:
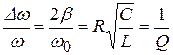 . (20.29)
. (20.29)
По (20.4) 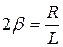 , тогда
, тогда 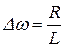 , и
, и
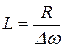 . (20.30)
. (20.30)
Дата добавления: 2015-09-07; просмотров: 1104;
