Теоретическое введение. Колебаниями называются процессы, характеризуемые повторяемостью во времени

Колебаниями называются процессы, характеризуемые повторяемостью во времени. Колебания, вызванные сообщением начального запаса энергии, называются свободными или собственными. Собственная частота колебательной системы w₀ определяется только параметрами системы.

Затухающими называются колебания, амплитуда которых уменьшается во времени, что объясняется потерями энергии в процессе свободных колебаний.

В начальный момент, когда конденсатор полностью заряжен, в нем накоплена электрическая энергия: . Во время разрядки конденсатора электрическая энергия превращается в энергию магнитного поля катушки, и когда конденсатор полностью разряжен, вся электрическая энергия переходит в магнитную:

,

где I₀ – наибольшая величина тока в контуре.

При перезарядке конденсатора энергия магнитного поля снова превращается в энергию электрического поля. В контуре возникают незатухающие электромагнитные колебания.

Проводники контура всегда обладают электрическим сопротивлением, поэтому часть энергии в процессе колебаний расходуется на нагрев проводников. Вследствие этого амплитуда электромагнитных колебаний в контуре постепенно уменьшается, и в нем происходят затухающие колебания (рис. 18.2). При достаточно большом сопротивлении контура или малой индуктивности колебания в нем вообще не возникают, а происходит так называемый апериодический разряд конденсатора (рис. 18.3).

По второму закону Кирхгофа можно записать:

; (18.1)

, (18.2)

где

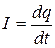. (18.3)

Так как 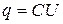, то из (18.1), (18.2) и (18.3) получаем:

.

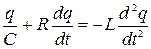Или после деления на L:

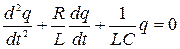. (18.4)

Полученное уравнение (18.4) является однородным дифференциальным уравнением второго порядка, оно описывает затухающие колебания. Приняты следующие обозначения:

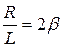, , (18.5)

тогда уравнение можно записать в стандартном виде:

, (18.4 а)

здесь β – коэффициент затухания, w₀ – частота собственных незатухающих колебаний контура (то есть частота свободных колебаний контура при отсутствии сопротивления R).

При не слишком большом затухании, то есть если β<w₀, решение уравнения (18.4) имеет вид:

, (18.6)

где циклическая частота затухающих колебаний ω равна:

, (18.7)

а амплитуда стечением времени уменьшается по экспоненте (рис.18.2):

A(t)=q₀e^-βt . (18.8)

При этом период колебаний

. (18.9)

Из (18.6) найдем напряжение на конденсаторе:

, (18.10)

Если (18.1) записать в виде: и продифференцировать по времени, то получим уравнение того же типа, что и уравнение (18.4):

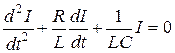, (18.4 б)

из чего следует, что ток в контуре также совершает затухающие колебания, для которых значения β, ω и Т определяются по формулам (18.5), (18.7) и (18.8):

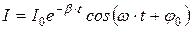. (18.11)

Тот же результат можно получить, продифференцировав по времени (18.6):

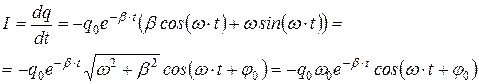(18.12)

Из формул (18.7) и (18.8) следует, что в контуре возможны затухающие колебания лишь в том случае, если 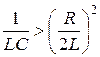(частота и период – действительные величины), или 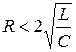. Если , то частота и период – мнимые, колебаний нет, и происходит апериодический разряд конденсатора (см. рис. 18.3).

Сопротивление

(18.13)

называется критическим.

Для характеристики степени затухания колебаний, кроме коэффициента затухания β, используется еще логарифмический декремент затухания.

Логарифмический декремент затухания – это натуральный логарифм отношения амплитуд двух следующих друг за другом колебаний:

, (18.14)

где колебания с номерами n и (n+1) отстоят друг от друга по времени на один период:

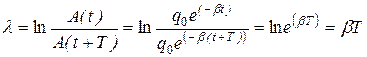. (18.15)

Очевидно, логарифмический декремент будет одинаков и для колебаний напряжения, и тока, и заряда на конденсаторе в нашем колебательном контуре, то есть:

(18.16)

или

. (18.16 а)

Так как 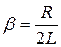(18.5), то:

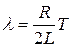. (18.17)

Еще одна важная физическая величина характеризует затухание колебаний – добротность:

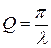. (18.18)

Можно показать, что добротность обратно пропорциональна относительной убыли энергии колебаний за время, равное одному периоду:

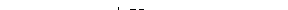
. (18.19)

В ряде случаев удобно изучать колебательный процесс в системе координат I и U, то есть откладывать по оси абсцисс величину тока в контуре в заданный момент времени, а по оси ординат – напряжение на конденсаторе в тот же момент времени. Плоскость U–I носит название плоскости состояний или фазовой плоскости, а кривая, изображающая зависимость напряжения от тока, называется фазовой кривой.

Найдем фазовую кривую для контура, сопротивление которого R=0. В этом случае 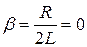и из (18.7), (18.10) и (18.12) имеем:

и 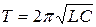(18.20)

; (18.21)

(18.21а)

Уравнения (18.21) и (18.21а) описывают незатухающие колебания. Исключив из них время t, получим уравнение фазовой кривой:

Это уравнение эллипса. Эллипс получается в результате сложения двух взаимно перпендикулярных гармонических колебаний (18.21) и (18.21а), сдвинутых по фазе на четверть периода. В контуре, сопротивление которого R>0, происходят затухающие колебания напряжения (18.10) и тока (18.12). В этом случае амплитуды напряжения и тока в контуре непрерывно убывают, не повторяясь через период времени, и фазовая кривая получается незамкнутой (рис.18.4).