Экспериментальная установка и методика измерений. Функциональная схема представлена на рисунке 18.5.

Функциональная схема представлена на рисунке 18.5.

При не очень больших значениях сопротивления контура ( , где L – индуктивность катушки, С – емкость конденсатора)), на экране осциллографа наблюдается картина затухающих колебаний, как это показано на рис.18.6, что соответствует закону изменения напряжения

.

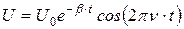Измерив амплитуды колебаний, отстоящие друг от друга на время, равное периоду:

,

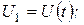
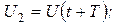
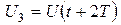можно определить логарифмический декремент затухания

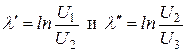(18.22)

и его среднее значение

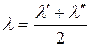. (18.23)

Или аналогично для тока:

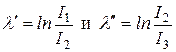. (18.22а)

Тогда коэффициент затухания можно рассчитать как

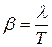. (18.24)

Значение сопротивления в контуре можно изменять с помощью магазина сопротивлений (R_маг.). Полное активное сопротивление контура R складывается из активного сопротивления катушки индуктивности R_кат. и сопротивления магазина R_маг.: 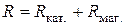. Из (18.17) 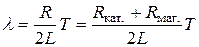получим, что зависимость l=f(R_маг.) логарифмического декремента затухания от сопротивления R_маг. в контуре линейная (рис.18.7).

Значение R_кат. можно определить, экстраполируя график до значения l®0. Индуктивность L катушки можно рассчитать по формуле (18.5) для коэффициента затухания:

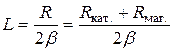(18.25)

и, считая b<<w₀, емкость С конденсатора из формулы Томсона (18.18):

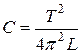. (18.26)

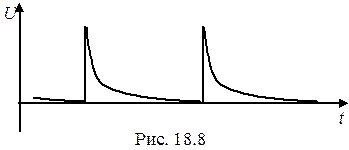
При больших значениях сопротивления контура ( 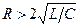) на экране электронного осциллографа будет наблюдаться апериодический процесс, показанный на рис.18.8.

Измерения логарифмического декремента затухания l можно проводить также с помощью фазовой кривой U=f(I). Если сопротивление контура , то фазовые кривые имеют вид, показанный на рис.18.4. При больших значениях сопротивления контура ( 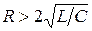) фазовая кривая для апериодического разряда принимает вид, показанный на рис.18.9.

В работе для получения колебаний в контуре используется модуль ФПЭ-10 с контуром, изображенным на рис.18.10. Если генератор задает частоту n_ген., то цикл подзарядки конденсатора длится 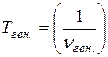секунд, этому времени на экране осциллографа соответствует отрезок d₁ (рис.18.6). Периоду колебаний T соответствует отрезок d. Следовательно, период затухающих колебаний может быть определен по формуле 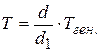, или:

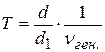. (18.27)

Сигнал в форме гармонического колебания заданной частоты с генератора PQ преобразователем ПИ преобразуется в последовательность прямоугольных импульсов той же частоты.

Будучи поданным на колебательный контур КК, импульс заряжает конденсатор С до напряжения U_m, сообщая контуру начальный запас энергии. По окончании импульса происходит многократный разряд конденсатора С через индуктивность L и сопротивление R, то есть возникают затухающие колебания (рис.18.6).

Изменение коэффициента затухания β колебательного процесса осуществляется выбором величины резистора R_маг. магазина сопротивления МС.