Предварительные сведения и определения.
 Трехфазной цепью называется объединение определенным образом в одну цепь трех однофазных цепей, удовлетворяющих соответствующим требованиям.
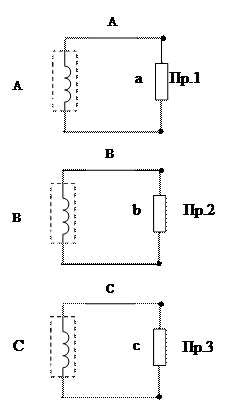
Трехфазной цепью называется объединение определенным образом в одну цепь трех однофазных цепей, удовлетворяющих соответствующим требованиям.
Рис.3.1
Каждая однофазная часть трехфазной цепи называется фазой этой цепи.
Фазы обозначаются буквами А,В,С. Заглавными буквами принято обозначать фазы генератора, а маленькими буквами – фазы приемника (рис. 3.1).
Для образования трехфазной цепи необходимо, чтобы фазы генератора удовлетворяли следующим требованиям:
1. ЕА=ЕВ=ЕС - электродвижущие силы, т.е. напряжения , генераторов однофазных цепей равны между собой.
2. φАВ= φВС= φСА=120о= 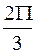 - фазы напряжений генераторов различных однофазных цепей (т.е. фаз) отличаются на треть периода, т.е. на 120о. (Следует понимать, что слово «фаза» употребляется в предыдущем предложении в двух разных смыслах: как аргумент синусоидальной функции напряжения, и как часть трехфазной цепи).
- фазы напряжений генераторов различных однофазных цепей (т.е. фаз) отличаются на треть периода, т.е. на 120о. (Следует понимать, что слово «фаза» употребляется в предыдущем предложении в двух разных смыслах: как аргумент синусоидальной функции напряжения, и как часть трехфазной цепи).
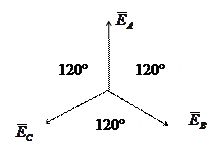 Векторная диаграмма напряжений генератора представлена на рис. 3.2:
Векторная диаграмма напряжений генератора представлена на рис. 3.2:
Рис. 3.2
Наиболее распространенными способами объединения однофазных цепей в трехфазную цепь являются способы : «звезда », обозначаемый обычно «Y», и «треугольник», обозначаемый «Δ ».
3.2.Способ объединения в трехфазную цепь «звезда–звезда»
 («Y-Y»)
(«Y-Y»)
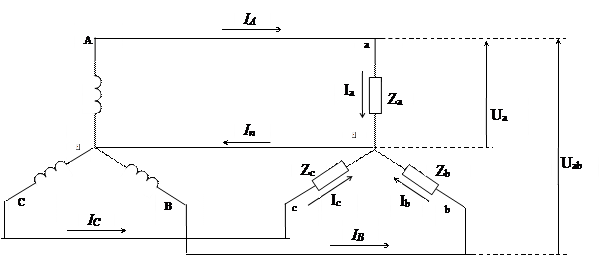
Рис. 3.3
На рис. 3.3: А,В,С – концы фаз генератора; а,b,с - концы фаз приемника;
Za, Zb, Zc - полные сопротивления соответствующих фаз приемника; точки N и n – так называемые нейтральные точки.
Провод Nn называется нейтральным проводом, а ток, текущий по нему – нейтральным током IN .
Провода Аа, Вв, Сс называются линейными проводами, а токи, текущие по этим проводам – соответствующими линейными токами, которые обозначаются IлA, IлВ , IлС .
Токи, текущие через фазы приемника, называются фазными токами и обозначаются Iфа, Iфb , Iфс .
Напряжения на фазах приемника называются фазными напряжениями и обозначаются Uфа, Uфb , Uфс. Фазное напряжение действует между нейтральным и соответствующим линейным проводом.
Напряжения, действующие между концами различных фаз приемника (или генератора), называются линейными напряжениями и обозначаются Uав, Uвс , Uса. Эти же напряжения действуют между линейными проводами.
Нагрузка (приемник) трехфазной цепи называется симметричной, если все три фазы приемника одинаковы, т.е. равны активные составляющие фаз приемника: Rа =Rв = Rс и равны реактивные составляющие фаз приемника: Xа =Xв = Xс , откуда следует, что равны и полные сопротивления фаз приемника: Zа Zв Zс . Однако следует понимать, что равенства полных сопротивлений фаз приемника недостаточно, чтобы этот приемник был симметричным, так как равенство полных сопротивлений еще не означает равенство активных и реактивных составляющих полного сопротивления.
Пример такого несимметричного приемника приведен на рис.3.4
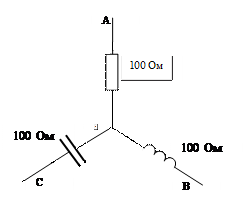 |
Рис. 3.4
3.2. Свойства соединения «звезда – звезда» («Y - Y»)
1. Линейные и фазные токи соответствующих фаз равны между собой :
IлA=Iфa; IлВ=Iфb; IлС=Iфс (3.1)
2. Все фазы приемника подключены параллельно к соответствующим фазам генератора (с помощью линейных проводов и нейтрального провода). Поэтому фазные напряжения приемника равны фазным напряжениям генератора, и, следовательно, равны между собой по величине:
Uа= Ub= Uс (3.2)
Разность фаз напряжений на фазах приемника равна 120°, или одной трети периода. Как и у генератора:
φаb= φbс= φса=120о = 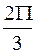 (3.3)
(3.3)
Таким образом, векторная диаграмма фазных напряжений приемника имеет вид, представленный на рис. 3.5, и представляет собой систему трех симметричных векторов:
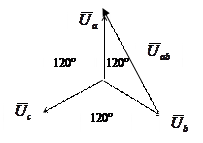 |
Рис.3.5
Замечание: Это свойство присуще трехфазной цепи при наличии нейтрального провода, а также при его отсутствии в том случае, если приемник симметричен. Другими словами, равенство фазных напряжений невозможно в случае несимметричной нагрузки при отсутствии нейтрального провода.
3. Линейные напряжения приемника, основываясь на знании второго закона Кирхгофа, можно представить как векторные разности соответствующих фазных напряжений (см. рис. 3.5) :
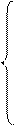
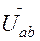 =
= 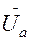 -
- 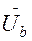
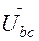 =
= 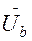 -
- 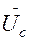 (3.4)
(3.4)
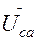 =
= 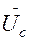 -
- 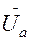
В частном случае симметричной нагрузки, или при несимметричной нагрузке, но при наличии нейтрального провода, то есть тогда, когда справедливо свойство 2, между линейными и фазными напряжениями существует соотношение:
Uл = 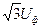 (3.5)
(3.5)
Студентам предлагается самостоятельно получить это соотношение, используя геометрические соотношения.
Следует обратить внимание, что соотношение (3.5) не справедливо, если нагрузка несимметрична при отсутствии нейтрального провода.
Условие (3.5) обязательно должно выполняться в электрических сетях, поэтому при несимметричной нагрузке обязательно наличие нейтрального провода. Отсутствие нейтрального провода допустимо только при заведомо симметричной нагрузке.
3.4. Последовательность расчета трехфазной цепи «звезда-звезда»:
3.4.1.Рассчитываются фазные токи по закону Ома:
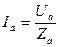 ;
; 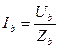 ;
; 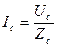 ; (3.6)
; (3.6)
Помимо токов необходимо рассчитать разности фаз фазных токов и соответствующих фазных напряжений:
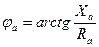 ;
; 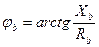 ;
; 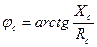 ; (3.7)
; (3.7)
3.4.2. Рассчитывается ток нейтрального провода в соответствии с первым законом Кирхгофа (см. схему на рис.3.3):
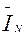 =
= 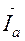 +
+ 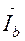 +
+ 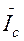 (3.8)
(3.8)
Для этого необходимо:
а) построить векторную диаграмму фазных напряжений.
б) дополнить ее векторами фазных токов
в) сложить векторы фазных токов.
Первым делом выбираем масштаб для тока (масштаб напряжения в данном случае не имеет значения, т.к. никакие действия с векторами напряжений выполняться не будут). Векторы токов откладываем в выбранном масштабе под рассчитанными по формулам (3.7) углами к фазным напряжениям. Затем выполняем векторное сложение. Измеряем длину результирующего вектора и, пользуясь масштабом тока, определяем ток в нейтральном проводе (рис.3.6). В приведенном примере:
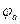 >0;
>0; 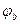 <0;
<0; 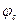 < 0
< 0
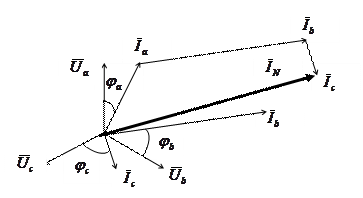 |
Рис. 3.6. Определение тока нейтрального провода с помощью векторной диаграммы
2.4. Частный случай: симметричный приемник.
Для симметричного приемника справедливо:
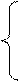 Ia = Ib = Ic
Ia = Ib = Ic
(3.9)
φа= φв= φс
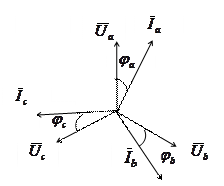 Это значит, что при симметричной нагрузке фазные токи образуют систему трех симметричных векторов (см. рис. 3.7) , сумма которых, то есть нейтральный ток, равна нулю. Это легко доказать геометрически, что и предлагается студентам сделать самостоятельно.
Это значит, что при симметричной нагрузке фазные токи образуют систему трех симметричных векторов (см. рис. 3.7) , сумма которых, то есть нейтральный ток, равна нулю. Это легко доказать геометрически, что и предлагается студентам сделать самостоятельно.
 |
Рис. 3.7
Вывод: При симметричной нагрузке нейтральный провод не нужен. Применяется так называемая трехпроводная линия, состоящая из трех линейных проводов.
Примерами симметричной нагрузки могут служить трехфазный электродвигатель, трансформатор. Эти виды электрооборудования подключаются тремя проводами. Во всех остальных случаях, когда нагрузка несимметрична, нейтральный провод обязателен. Роль нейтрального провода состоит в сохранении симметрии фазных напряжений.Отсутствие нейтрального провода при несимметричной нагрузке приводит к возникновению так называемого «перекоса фаз», а точнее, фазных напряжений – при этом в одних фазах напряжение возрастает, а в других – уменьшается. В связи с исключительной ролью нейтрального провода в нем запрещается устанавливать любые устройства защиты.
Дата добавления: 2015-10-09; просмотров: 1133;
