ЛЕКЦИЯ 2.

1.3.4 Преобразование «треугольник» - «звезда».

На рис. 1.5 показана одна из разновидностей мостовых схем, называемая четырехплечий мост или мост Уитстона . Ни одну пару сопротивлений в этой схеме нельзя квалифицировать как последовательно или параллельно включенные. Следовательно, к ней неприменимы основные правила нахождения эквивалентных сопротивлений. Расчет эквивалентного сопротивления схем такого типа осуществляется методом эквивалентных преобразований.

При эквивалентном преобразовании часть цепи заменяется новыми элементами с другим их соединением. При этом сопротивления новых элементов должны быть такими, чтобы проведенная замена не привела к изменению распределения токов и напряжений в участках цепи, не подвергшихся изменениям. В этом случае новую цепь можно считать эквивалентной старой.

Рассмотрим одно из широко распространенных эквивалентных преобразований - преобразование "треугольник - звезда". Участок цепи 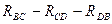.,ограниченный узлами В, С, D (рис. 1.4, слева), заменяется новыми элементами 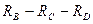соединенными по схеме

"трехлучевая звезда" и подключенными к тем же точкам исходной цепи В, С, D (рис. 1.4, справа); при этом в новой схеме, называемой схемой замещения, добавляется еще один узел - Е.

Рис. 1.4

Применим это преобразование для расчета эквивалентного сопротивления четырехплечего моста. Заменим резисторы R₃, R₄и R₅, включенные "треугольником" между узлами В, С и D (выделенная область на рис. 1.5), новыми резисторами R_B ,R_C ,R_D , соединенными в трехлучевую звезду (выделенная область на рис. 1.6. В результате замены элементов ток, вытекающий из узла В, и токи, втекающие в узлы С и D (токи I_B, I_Cи I_Dсоответственно), не должны измениться. Это значит, что не должна измениться проводимость схемы между узлами В-С, B-D и C-D.

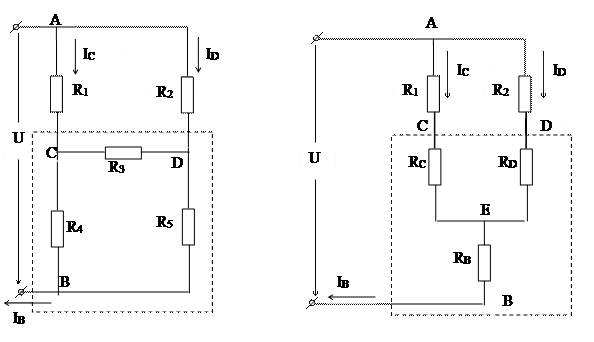
Рис. 1.5 Рис.1.6

Рассмотрим проводимость обеих схем между узлами В-С. В исходной схеме эта проводимость осуществляется по двум каналам протекания тока: через резистор R_A (его проводимость равна 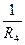) и через цепочку резисторов 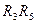(её проводимость равна ).

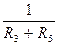Суммарная проводимость обоих каналов составляет 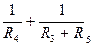. В схеме замещения проводимость между этими же узлами осуществляется по цепочке резисторов R_B R_C и равна 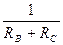. Проводимости в обеих схемах должны быть равными.

Аналогично рассматриваются проводимости в обеих схемах между узлами B-D и C-D. В итоге получаем систему из трех линейных уравнений с тремя неизвестными, которую можно разрешить относительно R_B, R_C, R_D, т.е. выразить последние через R₃, R₄ ,R₅ :

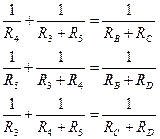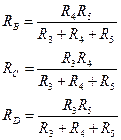=> (1.24)

Рассчитанная таким образом схема замещения по своим свойствам эквивалентна исходной схеме. Расчет эквивалентного сопротивления схемы замещения не представляет труда.

Заменим последовательную цепочку R₁R_C на один резистор R_1C , сопротивление которого равно сопротивлению этой цепочки, т.е.R₁+Rc. Аналогично заменим цепочку R₂R_D один резистор R_2D, сопротивление которого равно R₂+R_D. В схеме теперь можно выделить два параллельных элемента: R_1Cи R₂R_D. Заменим этот фрагмент схемы одним резистором R_1C2D. Эквивалентное сопротивление находится из уравнения

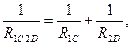(1.25)

т.е. 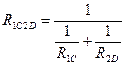. (1.26)

Теперь наша схема свелась к последовательному соединению элементов R_B и R_1C2D.

Окончательно получаем

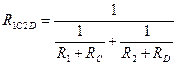(1.27)