Распределение ресурсов

Задано множество заказов А₁, А₂, …, А₅, стоимости которых в одинаковых единицах измерения равны, соответственно, 1; 1; 1; 2,6; 4. Также задано множество предприятий В₁, В₂, …, В₆— потенциальных изготовителей данных заказов, производственные мощности которых соотносятся как 1 : 1,2 : 1,4 : 1,5: 2 : 2,4. Каждое предприятие может участвовать в выполнении любого количества заказов и каждый заказ может выполняться любым числом предприятий.

Требуется найти оптимальное распределение заказов по предприятиям, при котором будет минимизировано общее время их выполнения.

Возможные варианты распределения заказов можно интерпретировать в виде набора взвешенных двудольных графов. Один из оптимальных вариантов дан на рис. 1.13.

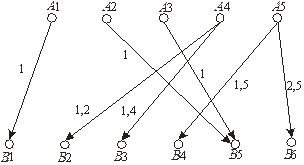
Рис.1.13. Один из оптимальных вариантов распределения

Задачи

1. Найти число рёбер в полном двудольном графе K_k,l .

2. При каком соотношении чисел вершин k и l в полном двудольном графе K_k,l возможно построение простого цикла, содержащего все вершины графа?

3. В полном двудольном графе K_4,5 веса ребер, соединяющих вершину V_i из первой доли с вершиной W_j из второй доли, приняты равными (i+j). Построить в полученном взвешенном графе минимальное остовное дерево по алгоритму Прима.

1.5. Единичные n—мерные кубы

Определение Единичным n — мерным кубом называется граф, у которого вершинам соответствует полный набор булевых векторов длины n, а рёбра соединяют между собой все вершины, соответствующие соседним наборам (которые различаются ровно по одной координате). Обозначается n — мерный куб Вⁿ.

Количество вершин в Вⁿ равно 2ⁿ. Примеры n — мерных кубов при n = 1, 2, 3 приведены на рис.1.14.

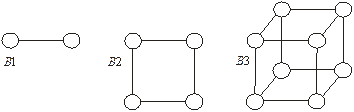
Рис.1.14. Примеры Вⁿ при n = 1, 2, 3.

В Разделе II даны определения сферы и шара в единичных n — мерных кубах, а также введено расстояние Хэмминга на множестве булевых векторов длины n. Рассмотрим примеры применения данного вида графов.