Комбинаторика. Теория вероятности

При помощи деревьев хорошо иллюстрируются методы подсчета чисел сочетаний. Допустим, необходимо найти все возможные способы размещения на трех позициях объектов из наборов {a} = {a₁, a₂, a₃}, {b} = {b₁, b₂, b₃, b₄} и {c} = {c₁, c₂} при условии, что на первой позиции может быть размещен один из объектов {a}, на второй ― один из объектов {b}, на третьей - один из {c}, размещения на позициях осуществляются независимо. Найти вероятность появления каждой комбинации при условии равновероятного данных событий.

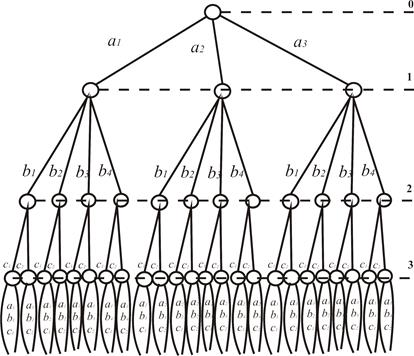
Рис.1.8. Полное множество размещений

Решение. Полное множество размещений получаем при помощи дерева, растущего из начальной вершины (корня) вниз.

а) Из корня (вершины нулевого уровня) проводим ребра, соответствующие всем объектам {a₁, a₂, a₃}из набора {a}. Получаем вершины первого уровня.

б) Из каждой вершины первого уровня проводим ребра, соответствующие всем объектам {b₁, b₂, b₃ , b₄}. Получаем вершины второго уровня.

в) Из вершин второго уровня проводим ребра, соответствующие объектам {c₁, c₂}. Полученные вершины третьего уровня описывают все искомое множество размещений.

Дерево на рис.1.8 показывает способ образования всех возможных комбинаций. Общее их число равно 3 × 4 × 2 = 24.

Ответ: вероятность появления каждой из комбинаций равна 1/24.