Псевдографы, графы, способы их задания

Рассмотрим некоторое множество элементов вида V_i (i = 1,…, n) и производное от него множество Х пар элементов из V вида (V_i , V_j), где(1 £ i, j £ n).

Определение. Элементы множества V называют вершинами. Еcли порядок следования элементов в парах Х = {(V_i , V_j), (1 £ i, j £ n)}не зафиксирован, то такие пары называют ребрами, а совокупность G = (V, X) ― неориентированным псевдографом. В том случае, когда все пары Х упорядочены, их называют дугами, а совокупность G = (V, X) ― ориентированным псевдографом.

Для краткости прилагательное «неориентированный» в названиях будет опускаться. Графически вершины обычно изображают точками или окружностями малого диаметра, рёбра ― линиями, дуги ― однонаправленными стрелками.

Определение. Если элементам—рёбрам (элементам-дугам) Х_ij = {(V_i , V_j)}псевдографа G = (V, X) присвоены некоторые числовые значения d_ij (1 £ i, j£ n), называемые весами рёбер (дуг), то псевдограф называют взвешенным.

Также веса ребер или дуг называют расстояниями. Множество всех весов задают матрицей D размером n ´ n, а весь взвешенный псевдограф обозначают как G = (V, X, D).

Пример 1. Псевдограф задан множествами V = (1, 2, 3); X = ((1,1), (1,1), (1,2), (1,2), (2,3), (3,3), (3,3)). Графическое изображение псевдографа дано на рис.1.1.

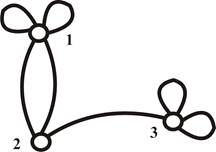
Рис.1.1. Псевдограф из примера 1

Пример 2. Ориентированный псевдограф задан множествами V = (1, 2, 3); X = ((1,1), (1,1), (1,2), (2,1), (2,3), (3,3), (3,1)). Графическое изображение дано на рис.1.2.

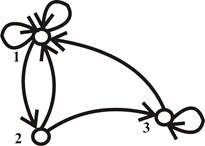
Рис.1.2. Ориентированный псевдограф из примера 2

Определение. Элементы ― рёбра (элементы ― дуги) X вида (V_i , V_i ), соединяющие одну и ту же вершину, называют петлями. Псевдограф без петель называют мультиграфом.

Пример 3. Мультиграф, имеющий множества вершин и рёбер V = (1, 2, 3), Х = ((1, 2), (1, 2), (2, 3)), показан на рис.1.3.

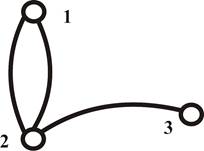
Рис.1.3. Мультиграф из примера 3

Определение. Если в множестве рёбер (дуг) X есть одинаковые элементы, то их называют кратными. Мультиграф без кратных ребер называют графом. Ориентированный граф для краткости обозначения называют также орграфом.

Пример 4. V = (1, 2, 3), X = ((1, 2), (2, 3)). На рис.1.4 показан граф и орграф с данными множествами (V, X).

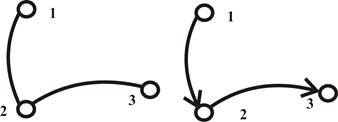
Рис.1.4. Граф и орграф из примера 4

Определение. Если вершины графа (орграфа) V_i и V_j соединены ребром (дугой) Х_k = (V_i , V_j),то их называют смежными. Вершина V_i и ребро (дуга) Х_k = (V_i, V_j), образованные данной вершиной, называют инцидентными. Степенью вершины V называются число d(V) ребер (дуг), инцидентных ей. Если d(V) = 0, то вершину называют изолированной, если d(V) = 1, то ― висячей.

В примере 3: d(V₁)=2, d(V₂)=3, d(V₃)=1, вершина V₃― висячая.

Определение. Рассмотрим граф G=(V, X). Граф G₁ = (V₁, X₁) называют подграфом графа G, если V₁Í V, Х₁ Í Х.

Определение. Последовательность вершин и ребер, связывающих их, называется маршрутом (путем). Число ребер в маршруте называется длиной маршрута. Маршрут, в котором все ребра попарно различны, называется цепью. Цепь, в которой все вершины попарно различны, различны, называется простой цепью. Маршрут, в котором начальная и конечная вершины совпадают (V₁= V_n), называется циклом. Цикл, в котором кроме V₁ и V_n все вершины различны, называется простым.

В примере 3 последовательность (V₁Х₁ V₂ Х₃ V₃) ― маршрут из вершины V₁в вершину V₃.

Пример 5. V = (1, 2, 3, 4), X = ((1, 2), (1, 3), (1, 4), (2, 3), (2,4), (3, 4)). Граф показан на рис.1.5. Номера ребер заданы числами 1–6.

Рис.1.5. Граф из примера 5

В графе выделены следующие циклы:

(V₁ 1 V₂ 2 V₃ 3 V₄ 6 V₂ 1 V₁) ― цикл длины 5,

(V₁ 1 V₂ 2 V₃ 3 V₄ 4 V₁) ― простой цикл длины 4.

Определение. Граф (орграф) называется связным, если для любых двух его вершин существует цепь, соединяющая их.