Способы задания графов (орграфов)
1. Списки вершин и рёбер (дуг).Множества V и X задают путём перечисления их элементов. Способ рассмотрен в вышеприведенных примерах.
Для практической работы с графами их представляют в памяти вычислительных устройств в матричной форме. В основном используют две матричных формы.
2. Матрица смежности.
Определение. Матрицей смежности графа G = (V, X), имеющего n вершин V1, ... ,Vn , называют квадратную матрицу А размерами n´ n, у которой каждой строке с номером i (столбцу с номером j) соответствует вершина с номером i (j). Если вершины Vi и Vj смежные, то элемент аi j =1, иначе аi j = 0.
Замечание. У неориентированных графов матрицы смежности симметричны (аij =аji) и их диагональные элементы равны нулю: аi i = 0.
Матрица инцидентности.
Определение. Матрицей инцидентности графа (орграфа) G = (V, X), имеющего n вершин V1 , . . . , Vn и m рёбер (дуг) Х1, ... , Хm , называют матрицу B размерами n´ m, у которой строкам соответствуют вершины, а столбцам ― рёбра (дуги). Если вершина Vi инцидентна с ребром (дугой) Хj , то элемент аi j = 1, иначе аi j = 0.
Задачи
1. Доказать, что в любом связном графе с n вершинами должно быть не менее (n-1) ребра.
2. Построить матрицы смежности и инцидентности для графов, заданных списками:
а) V = (1, 2, 3), X=((1, 2), (1, 3)),
б) V = (1, 2, 3, 4), X = ((1, 2), (1, 3), (1, 4), (2, 3)),
в) V = (1, 2, 3, 4, 5), X = ((1, 3), (1, 5), (2, 4), (2, 5), (3, 4), (4, 5)),
г) V = (1, 2, 3, 4, 5, 6), X = ((1, 3), (1, 4), (1, 6), (2, 4), (2, 5),(3, 5),(3, 6), (4, 6)).
3.Построить матрицы смежности и инцидентности для графа из примера 5.
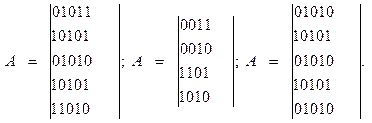 |
4.Построить матрицы инцидентности для графов, имеющих следующие матрицы смежности:
Использование графовых представлений систем позволяет более наглядно представить их структуру, выявить свойства, пояснить методы исследования. Рассмотрим основные виды графов и примеры их применения в исследовании систем разного рода.
Дата добавления: 2015-10-05; просмотров: 1844;
