Проектирование РС

Рассмотрим проектирование физической структуры РС по заданной функции проводимости. Наиболее употребительным критерием оптимальности РС является минимальность общего числа контактов РЭ, входящих в схему, поскольку при этом повышается надежность схемы, снижается вес, габариты, себестоимость, энергопотребление.

Аналогичный критерий оптимальности был ранее рассмотрен для нормальных форм. Оптимальные по нему формы называют минимальными. Однако, если отказаться от обязательного представления формул в нормальной форме, то можно получить и более оптимальные их варианты с точки зрения уменьшения в них числа переменных. Для этого в МДНФ и МКНФ необходимо дополнительно использовать дистрибутивные законы алгебры логики, которые являются аналогами правил вынесения за скобки:

x & y Ú x & z = x &(y Ú z);

( x Ú y ) & ( x Ú z) = x Ú y & z.

Также при оптимизации схем также часто применяют правила поглощения:

x ( х Ú y ) = x ;

x Ú x y = x .

В данных законах вместо x , y , z могут быть подставлены любые формулы. При наличии нескольких вариантов использования данных законов следует выбирать те, которые обеспечивают сокращение наибольшего числа переменных в формуле.

Определение. Оптимальными в классе нормальных форм будем называть РС, соответствующие МДНФ либо МКНФ, построенным по заданной функции проводимости. Абсолютно оптимальными будем называть РС, полученные при максимальном сокращении числа переменных в соответствующих формулах.

Пример. Построить 1) оптимальную в классе нормальных форм и 2) абсолютно оптимальную РС, реализующие функцию проводимости ¦ = (01001100).

Решение.Обозначим РЭ схемы через Х, Y, Z. СДНФ функции имеет следующий вид :

¦ =`x`y z Ú x`y `z Ú x`y z .

МДНФ имеет вид: ¦ =`x`y z Ú х`y. Она содержит 5 символов переменных. Принципиальная схема РС, реализующей данную формулу будет следующей:

Рис.1.13

Соответствующая ей физическая схема имеет вид:

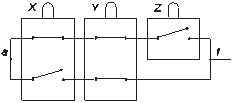
Рис.1.14

Полученная схема будет оптимальной в классе нормальных форм. Применение дистрибутивного закона к найденной выше МДНФ позволяет сократить её и даёт формулу: ¦=`y & (`x z Ú х ), которая содержит только 4 символа переменных. Следовательно, приведенная выше РС не является абсолютно оптимальной. Принципиальная и физическая схемы абсолютно оптимальной РС даны на рис.1.15 а) и б).

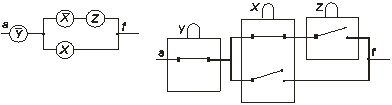
а) б)

Рис.1.15

При оптимизации физической структуры существующей РС вначале по ней строится соответствующая формула алгебры логики. Затем с использованием формульных преобразований или таблицы истинности определяется МДНФ либо МКНФ. Если необходимо, далее формула сокращается с использованием дистрибутивных и других законов алгебры логики.

Для построения оптимальных РС при частичном задании их функций проводимости вначале ЧОФ необходимо доопределить оптимальным образом.

ЗАДАЧИ

1. Построить оптимальные РС, реализующие функции:

а) х у Ú y z Ú x z ;б) х½ (у ® z) ;в) (х® у)&( y® z) ;г) х у Å xz ;д) (10011101);е) (01101110);ж) (0110100010010111) .

2. Найти функции проводимости, оптимизировать РС, схемы которых указаны на: а) рис. 1.16 ; б) рис. 1.17.

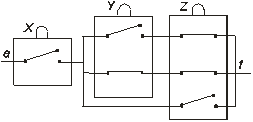
Рис.1.16

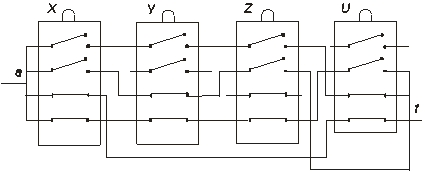
Рис.1.17

3. Построить оптимальные РС для частично определенных функций а) (0??011??) ; б) (?0?0?111) ; в) (1?0101??).

4. Обозначить РЭ, их контакты и построить РС, блокирующую главный привод аппарата в следующих случаях: а) открыт загрузочный или разгрузочный люк, б) давления в рабочей ёмкости или в рубашке отклоняются от допустимых пределов, в) рабочая ёмкость загружена менее чем на 1/4 полезного объёма.

5. Система управления приводами П1 и П2 содержит два датчика Д1 и Д2. При включенном Д1 и отключенном Д2 оба привода включаются, при включенном Д2 и отключенном Д1 включен только П1. В остальных случаях оба привода отключены. Построить управляющую РС.

6. Освещение в помещении должно включаться ровно одним из трех переключателей. Построить функцию проводимости и соответствующую РС.