Релейные схемы. Связь их физической структуры и функций проводимости с алгеброй логики
Анализ и синтез релейных управляющих схем
Релейные схемы (РС) являются одними из наиболее простых и распространенных в технике устройств управления. Отличительно особенностью РС является дискретный логический принцип срабатывания их элементов, реагирующих на внешние воздействия по принципу ”включен - выключен”. Это позволяет при анализе существующих схем и проектировании новых использовать методы алгебры логики.
Релейные схемы. Связь их физической структуры и функций проводимости с алгеброй логики
Со структурной точки зрения в РС можно выделить входы` а =(а1, ... аn ), задающие внешние воздействия на схему, выходы`f = (f1, ..., fm ), а также само релейное устройство (РУ):
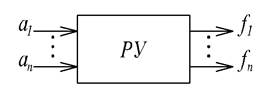
Рис.1.7
Значения компонент аi,¦j векторов`а и`¦ изменяются скачкообразно, принимая два состояния, которые можно без ограничения общности закодировать с помощью 0 и 1. Обычно при отсутствии тока состояние кодируют нулем, а после достижения порогового значения - единицей.
РУ состоят из дискретно срабатывающих релейных элементов (РЭ), реагирующих на внешние воздействия, и соединений между ними, а также с входами и выходами РС. Будем рассматривать РС наиболее простого типа с одним входом и одним выходом. Обычно их назначение заключается в подаче питания на исполнительный электродвигатель.
Релейные элементы по принципу действия делят на контактные и бесконтактные. В первых набор контактов замыкается либо размыкается при механическом нажатии на некоторый переключатель. В бесконтактных РЭ положение контактов изменяется при наличии электрических, магнитных, тепловых и других воздействий заданного уровня.
Поскольку с точки зрения анализа и синтеза РС конструктивное исполнение РЭ несущественно, будем обозначать последние в виде механических реле, содержащих две группы контактов – нормально замкнутых и нормально разомкнутых.
На рис.1.8 схематически показан РЭ, обозначенный Х и имеющий оба вида контактов: х1 – нормально разомкнутый (в свободном состоянии проводимость отсутствует, при нажатии на кнопку - появляется) и х2 – нормально замкнутый (в свободном состоянии проводимость есть, в нажатом - отсутствует). С точки зрения булевой алгебры контакту х1 соответствует тождественная функция х, поскольку в нем проводимость совпадает с наличием внешнего воздействия. Контакт х2 реализует функцию отрицания`x, так как при отсутствии воздействия проводимость у него есть, а при нажатии на переключатель цепь разрывается.
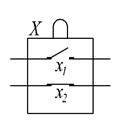
Рис.1.8
Функционирование РУ полностью определяется состоянием РЭ, входящих в них, и способом их соединения между собой. Пусть РС содержит n РЭ. Обозначим их Х1, … , Хn. Нормально разомкнутым контактам каждого реле Хi (1£ i £ n) ставим в соответствие переменную хi, нормально замкнутым контактам Хi - отрицание`хi. Различные контакты одного реле, принадлежащие к одной группе (замкнутые или разомкнутые), входят в разные цепи и если по одним проводимость есть, то по другим ее может не быть. Обозначим проводимость в общей цепи от входа к выходу РС через ¦. Если общая цепь замкнута, то ¦ = 1, иначе ¦ = 0.
При таком способе кодирования текущего состояния контактов РЭ и общей проводимости в РС ¦ последняя является булевой функцией переменных х1, ... , хn и их отрицаний. Поскольку РС в большинстве своем представляют электрические схемы, то данное отображение ¦(х1, ... , хn) обычно называют функцией проводимости.
Таким образом, функциональные свойства РС с одним входом и одним выходом однозначно описываются её булевой функцией проводимости ¦(х1, ... , хn).
Рассмотрим, каким образом характер соединений между контактами РЭ определяет функцию проводимости. На рис.1.9 показано последовательное соединение двух контактов Х и Y. Каждый из них может быть как замкнутым, так и разомкнутым. Схема реализует логическую операцию умножения &, так как функция проводимости равна единице тогда и только тогда, когда одновременно есть проводимость в обоих контактах Х и Y.
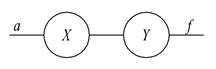
Рис.1.9
В случае параллельного соединения (рис.1.10) контактов схема реализует логическое сложение «ИЛИ», поскольку для выполнения условия ¦ = 1 достаточно выполнения хотя бы одного из условий Х =1 либо Y =1.
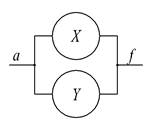
Рис.1.10
Физическая структура РС, в которой используются только параллельные и последовательные соединения, изоморфна некоторой формуле алгебры логики, отражающей наличие контактов РЭ в схеме, вид и порядок их соединения. Изоморфный характер отображения означает, что каждому нормально разомкнутому или замкнутому контакту РС взаимно однозначно соответствует своя переменная формулы либо ее отрицание, а для каждого соединения между контактами РС в формуле есть своя элементарная функция, стоящая между соответствующими выражениями формулы. На рис.1.11 приведена принципиальная схема РС, изоморфная формуле алгебры логики F(х, у) =`х & у Ú x.
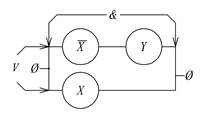
Рис.1.11
Как и в алгебре логики, где одна и та же функция может быть реализована множеством различных формул, у РС для обеспечения заданной функции проводимости могут быть использованы различные физические структуры. Поэтому все вопросы анализа, синтеза и оптимизации РС можно свести к изучению соответствующих им функций и формул в алгебре логики.
Замечание. Структура формул алгебры логики позволяет изоморфно отобразить только системы с параллельными и последовательными соединениями элементов (в данном случае – контактов РЭ). Схемы со смешанным порядком соединения элементов, которые нельзя эквивалентно преобразовать только к параллельным и последовательным соединениям, нельзя изоморфно отобразить формулами алгебры логики. Например, для схемы с 6 контактами РЭ, показанной на рис.1.12, не существует изоморфной формулы алгебры логики, содержащей 6 обозначений переменных и их отрицаний. Наиболее короткая формула для функции проводимости данной схемы, например, ¦ = x(y z Ú`y`z) Ú`x `z содержит 7 таких символов.
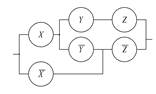
Рис.1.12
Дата добавления: 2015-10-05; просмотров: 1385;
