Операции суперпозиции и замыкания. Полнота, базис системы функций
Однотактные (не содержащие элементов памяти) дискретные логические устройства реализуют на выходе некоторый набор функций алгебры логики `Fm=(F1,F2,…,Fm), которые в каждый момент времени зависят только от состояния входов устройства `хn=(x1,x2,…,xn): `Fm = `Fm (`хn). Практически такие устройства проектируют и изготавливают из отдельных неделимых элементов, реализующих некоторый набор (систему) {f} элементарных функций алгебры путем присоединения выходов одних элементов ко входам других.
При проектировании логических устройств актуальными являются следующие вопросы.
1. Задана система элементарных функций {f}. Какие выходные функции Fi можно получить, используя функции из {f}?
2. Задано множество выходных булевых функций {F} (в частности, равное всему множеству функций алгебры логики Р2). Какой должна быть исходная система элементарных функций {f}, обеспечивающая возможность получения на выходе любой из функций множества {F}?
Для обоснованного ответа на данные вопросы используют понятия суперпозиции, замкнутости и полноты систем функций.
Определение. Рассмотрим множество логических связок {F}, соответствующее некоторой системе функций {f}. Суперпозицией над {f} называется любая функция j, которую можно реализовать формулой над {F}.
Практически суперпозицию можно представить как результат подстановки функций из {f} в качестве аргументов в функции из этого же множества.
Пример 1. Рассмотрим систему функций {f}={f1(х) =`х , f2 (х,у)= х&у, f3(х,у)= хÚу }. Подставляя в функцию f3 (х,у) вместо первого аргумента х функцию f1(х), вместо второго — f2 (х,у), получим суперпозицию h(х,у)= f3 (f1(х), f2(х,у))=`х Ú х & у. Физическая реализация подстановки дана на рис.1.18.
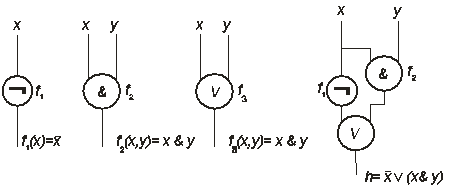
Рис.1.18
Определение. Пусть М —некоторое множество функций алгебры логики(P2). Множество всех суперпозиций над М называется замыканием множества М и обозначается [М]. Получение [М]по исходному множеству М называется операцией замыкания. Множество М называется функционально замкнутым классом, если [М] = М. Подмножество m Í M называется функционально полной системой в М, если [m] = М.
Замыкание [М]представляет собой все множество функций, которое можно получить из М путем применения операции суперпозиции, т.е. всех возможных подстановок.
Замечания. 1. Очевидно, любая система функций {f} является функционально полной в себе самой.
2. Без ограничения общности можно считать, что тождественная функция f(х)=х, не изменяющая значений истинности переменных, изначально входит в состав любой системы функций.
Пример 2. Для рассмотренных ниже систем функций {f} выполнить следующие действия:
1) найти замыкание [f ],
2) выяснить, будет ли система {f} замкнутым классом,
3) найти функционально полные системы в {f}.
Решение.
I. {f}={0}. При подстановке функции {fº0} в саму себя получаем ее же, т.е. никаких новых функций не образуется. Отсюда следует: [f] = {f}. Рассмотренная система является функционально замкнутым классом. Функционально полная система в ней одна и равна всей {f}.
II. {f}={0,Ø }. Подстановка Ø (Ø х)дает тождественную функцию, которая формально не расширяет исходную систему. Однако при подстановке Ø (0) получим тождественную единицу — новую функцию, которой не было в исходной системе: Ø (0)=1. Применение всех других подстановок не приводит к появлению новых функций, например: ØØ 0=0, 0(Ø х)=0.
Таким образом, применение операции суперпозиции позволило получить более широкое по сравнению с исходным множество функций [f]={0,Ø ,1}. Отсюда следует строгое вхождение: {f} Ì [f]. Исходная система {f}не является функционально замкнутым классом. Кроме самой системы {f}других функционально полных систем в ней нет, поскольку в случае её сужения из одной функции f=0 нельзя путем подстановки получить отрицание, а из одной функции отрицания нельзя получить тождественный нуль.
III. {f} = {& ,Ú ,Ø }.Замыканием данной системы является все множество функций алгебры логики P2, так как формулу любой из них можно представить в виде ДНФ либо КНФ, в которых используются элементарные функции {f} = {& ,Ú ,Ø}. Данный факт является конструктивным доказательством полноты рассмотренной системы функций в P2: [f] =P2.
Поскольку в P2 содержится бесконечное множество других функций, отличных от {f} = {& ,Ú ,Ø }, то отсюда следует строгое вхождение: {f}Ì[f]. Рассмотренная система не является функционально замкнутым классом.
Помимо самой системы функционально полными в ней будут подсистемы {f}1 = {& ,Ø } и {f}2= {Ú ,Ø }. Это следует из того, что при помощи правил де Моргана функцию логического сложения Úможно выразить через {& ,Ø},а функцию логического умножения & — через {Ú, Ø}:
(х & у) = Ø (`хÚ`у), (х Ú у) = Ø (х &`у).
Других функционально полных подсистем в {f} нет.
Проверку полноты подсистемы функций {f}1 Ì {f}во всей системе {f}можно производить путем сведения {f}1 к другой, заведомо полной в {f}системе.
Неполноту подсистемы {f}1 в {f}можно проверить, доказав строгое вхождение [f1] Ì [f].
Определение. Подмножество m Í M называют функциональным базисом (базисом) системы М, если [m] = М , а после исключения из нее любой функции множество оставшихся не полно в М .
Замечание. Базисами системы функций {f} являются все ее функционально полные подсистемы {f}1, которые невозможно уменьшить без потери полноты в {f}.
Пример 3. Для всех систем, рассмотренных в Примере 2, найти базисы.
Решение.В случаях 1 и 2 функционально полными являются только сами системы и сузить их невозможно. Следовательно, они же являются и базисами.
В случае 3 есть две функционально полные в {f}подсистемы {f}1 = {&,Ø } и {f}2={Ú,Ø }, которые невозможно сократить без потери полноты. Они будут базисами системы {f} = {&,Ú,Ø}.
Определение. Пусть система {f}является замкнутым классом. Ее подмножество {f}1 Ì {f}называют предполным классом в {f}, если {f}1 не полно в {f} ([f1] Ì [f]), а для любой функции jиз системы{f}, не входящей в {f}1(jÎ{f} \ {f}1) справедливо: [j È {f}1] = [f], т.е. прибавление jк {f}1 делает ее полной в {f}.
Задачи
1. Проверить замкнутость множеств функций:
а) {Ø }; б) {1, Ø }; в) {(0111); (10)};г) {(11101110); (0110)};д) {(0001); (00000001); (0000000000000001); … }.
2. Проверить полноту систем функций в P2:
а) {0,Ø }; б) {(0101) , (1010) }; в ) {¯ }; г ) {(0001) , (1010) }.
3. Найти замыкание системы функций и ее базис:
а) {0 , 1 , Ø }; б) {(1000) , (1010), (0101) }; в) {(0001) , (1110), ( 10) }; г ) {(1010) , (0001), (0111) }.
1.10.2 Функции, сохраняющие константы. Классы Т0 и Т1
Определение. Функция f(`хn) сохраняет 0, если f (0,..., 0) = 0. Функция f(`хn) сохраняет 1, если f(1, ... , 1) = 1.
Множества функций n переменных, сохраняющих 0 и 1, обозначают, соответственно, Т0nи Т1n. Все множества функций алгебры логики, сохраняющих 0 и 1, обозначают Т0 и Т1. Каждое из множеств Т0и Т1 является замкнутым предполным классом в Р2.
Из элементарных функций в Т0и Т1одновременно входят, например, &и Ú. Принадлежность любой функции к классам Т0 , Т1 можно проверить по первому и последнему значению ее вектора значений в таблице истинности либо непосредственной подстановкой нулей и единиц в формулу при аналитическом задании функции.
Определение. Дублирующей называют такую подстановку, при которой вместо нескольких независимых переменных в функцию подставляют одну и ту же переменную. При этом величины переменных в наборах, которые раньше принимали значения независимо друг от друга, всегда будут одинаковыми.
ЗАДАЧИ
1.Проверить принадлежность к классам Т0 и Т1 функций:
а) обощенного сложения, б) обощенного умножения, в) констант, г) ху Ú yz , д) х ® у ® ху , е) х Å у , ж)( х1Å… Å хn) ® ( y1Å… Å ym) при n,mÎ N.
2. Доказать замкнутость каждого из классов Т0 и Т1.
3. Доказать, что если f (`х n) ÏТ0, то из нее путем дублирующей подстановки можно получить константу 1 либо отрицание.
4. Доказать, что если f (`х n) ÏТ1 , то из нее путем дублирующей подстановки можно получить константу 0 либо отрицание.
5. Доказать предполноту каждого из классов Т0 и Т1 (например, сведением дополненной системы к {f} = {& ,Ú ,Ø } ).
6. Найти мощность классов Т0nи Т1n.
Дата добавления: 2015-10-05; просмотров: 2267;
