Метод Стокса

Рассмотрим свободное падение шарика в вязкой жидкости. На шарик действуют три силы: сила тяжести, выталкивающая (Архимедова) и сила сопротивления, зависящая от скорости.

Найдем уравнение движения шарика в жидкости. По второму закону Ньютона

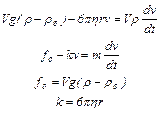(7)

где V – объем шарика,r – его плотность, r_ж – плотность жидкости, q– ускорение силы тяжести.

Интегрируя получим

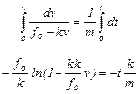
или после потенцирования

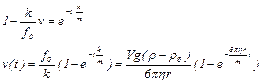(8)

Как видно из полученного выражения скорость шарика вначале увеличивается по экспоненциальному закону до предельного значения V_пред = 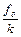. Экспонента очень сильно зависит от своего показателя. Практически после того, как показатель достиг значения –1, она быстро обращается в нуль. Поэтому можно считать, что скорость достигает предельного значения в течение времени t, за которое показатель экспоненты в (8) становится равным –1,т.е. это значение может быть найдено из условия 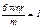, откуда

^.

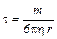В вязких жидкостях тела с небольшой плотностью могут достигать критических скоростей очень быстро.

Измеряя на опыте установившуюся скорость падения шариков можно определить коэффициент внутреннего трения жидкости по формуле

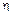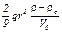= . (9)

Эта формула справедлива для шарика, падающего в безгранично простирающейся жидкости. Поэтому в формулу для h вводится поправочный множитель

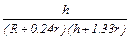, (9)’

где R – радиус центра, h– высота жидкости в нем (учитывая влияние стенок и дна цилиндра на падение шарика.

Заметим, что коэффициент внутреннего трения жидкости зависит от температуры

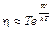, (10)

где Т – температура жидкости, W – энергия активации, K – постоянная Больцмана. Следовательно, с ростом температуры, особенно в области низких температур, вязкость жидкостей быстро уменьшается в то время, как для газов растет.