Теоретическое введение. В работе изучается динамика вращательного движения

В работе изучается динамика вращательного движения. В частно­сти, экспериментально проверяется уравнение моментов для вращения вокруг неподвижной оси

Iω = М_внеш, (1)

где I — момент инерции тела; ω — угловое ускорение М_внеш – сумма проекций на ось вращения моментов внешних сил.

На рис. 2 схематически показан прибор, с помощью которого удобно исследовать уравнение (1). Он называется маятником Обербека. Четыре спицы укреплены на втулке под прямым углом. На спицах находятся грузы массой m_гр каждый. Втулка и два шкива радиусами r₁ и r₂ насажены на общую ось. Ось закреплена в подшипниках так, что вся система может вращаться вокруг горизонтальной оси. Передвигая грузы по спицам, можно легко изменять момент инерции I тела. На шкив намотана нить, к которой привязана платформа известной массы. На платформу кладется груз, нить натягивается и создает вращающий момент

M=Tr_i, (2)

где Т – сила натяжения нити, r₁ — радиус шкива (г_i равен r₁ или r₂). Силу Т можно найти из уравнения движения платформы с грузом:

mg–T=ma, (3)

где m — масса платформы с грузом, а — ее ускорение. Ускорение а связано с угловым ускорением ε = 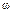соотношением

ε =а/r. (4)

Из уравнений (2) и (3) получаем, что момент силы натяжения нити

М = Тг=m(g — а)r. (5)

Кроме того, на маятник действует момент силы трения в оси M_тр.

С учетом этого уравнение (1) имеет вид:

m(g–a)r–M_тр=Ia/r . (6)

В уравнение (6) входит ускорение (а) платформы. Это ускорение можно довольно просто определить.

Действительно, измеряя время t, в течение которого платформа с грузом опускается на расстояние h, можно найти ускорение а:

a=2h/t². (7)

Тогда

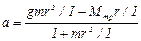(8)

Формула (8) дает связь между ускорением а, которое можно измерить опытным путем, и моментом инерции I. В формулу (8) входит неизвестная величина — момент силы трения M_тр. Хотя интуитивно понятно, что

момент силы трения мал, тем не менее он не настолько мал, чтобы им в (8) можно было полностью пренебречь. Если положить M_тр = 0, то можно убедиться, что результаты опыта будут отличаться от зависимости (8). Можно по порядку величины экспериментально определить М_тр и это нужно, конечно, сделать в начале работы. Для этого, с помощью нескольких грузов увеличивая силы натяжения Т нити, найдите минимальное значение массы m₀, при которой маятник начнет вращаться. Дальнейшие измерения нужно проводить с грузами массой m≥10m₀. На первый взгляд относительную роль момента силы трения можно уменьшить, если взять грузы массой m>> m₀, допустим, груз m= 10³m₀. Однако это не так по двум причинам. Первая — увеличение массы груза приводит к увеличению силы давления N на ось, а значит и к росту момента силы трения М_тр = μNr, где μ — коэффициент трения, r – плечо силы трения. Вторая причина состоит в том, что увеличение m уменьшает время падения t, а значит, ухудшает точность измерения ускорения а [см. (8)].

Момент инерции, входящий в (8), согласно теореме Гюйгенса— Штейнера может быть записан в виде:

I = I₀ + 4m_грR². (9)

Здесь R – расстояние центров грузов m_гр от оси вращения, I₀=I (R=0), т.е. равен моменту инерции системы при R= 0.

В (8) входит также отношение:

.

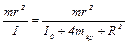В условиях опыта оно меньше или порядка 10^–2 (убедитесь в этом!). Пренебрегая этой величиной в знаменателе выражения (8). получаем формулу, которую можно проверить экспериментально:

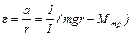(10)