Измерения. Представляет интерес экспериментально исследовать две зависимости.

Представляет интерес экспериментально исследовать две зависимости.

Первая — зависимость углового ускорения ε от момента внешней силы М = mgr при условии, что момент инерции I остается постоянным.

Если на оси ординат откладывать угловое ускорение е, а на оси абсцисс — mgr, то, согласно (10), экспериментальные точки должны ложиться на прямую. Из (10) видно, что наклон этой прямой равен 1/I, а точка пересечения с осью абсцисс дает М_тр.

Если экспериментальные данные подтверждают линейную зависимость ε от mgr, то можно приступить к изучению второй зависимости — зависимости момента инерции I от расстояния R грузов m_гр до оси вращения маятника (рис. 1).

Согласно теореме Гюйгенса—Штейнера:

I(R) =I_о + 4m_грR².

Выясним, как проверить эту зависимость экспериментально. Для этого преобразуем соотношение (10), пренебрегая в нем малой величиной (моментом силы трения М_тр) по сравнению с моментом mgr. Из (10) имеем:

.

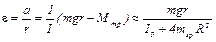Следовательно

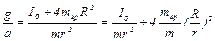(11)

Из (11) понятно, как экспериментально проверить зависимость (11): нужно, выбрав постоянную массу m груза, измерять ускорение а при различных положениях R грузов m_гр на спицах. Результаты измерений удобно изобразить в виде точек на координатной плоскости ХОУ, где х = (R/r) ², у = g/а.

Если экспериментальные точки в пределах точности измерений ложатся на прямую, то это подтверждает зависимость (11), а значит, и формулу

I(R)=I₀+4m_грR².

Отметим, что при выводе формулы (11) мы пренебрегли моментом сил трения, т.е. считали, что М_тр << mgr. Значение М_тр получено из графика зависимости ε = ε (mgr) при R = const. Это и позволяет выбрать массу перегрузки так, чтобы неравенство mgr >> М_тр заведомо выполнялось.

Роль момента сил трения можно оценить и иначе. Для этого заметим, что если маятник в начальный момент вращается с угловой скоростью ω₀, то к моменту остановки он повернется на угол φ, определяемый из соотношения

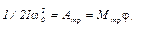(12)

где 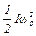– начальная кинетическая энергия вращающегося маятника,

А_тр — работа сил трения.

В (12) предполагается, что момент сил трения является постоянной величиной и связан с угловым ускорением соотношением

I ε₀=M_тр, (13)

где ε ₀ — ускорение, определяемое только моментом сил трения.

Из (12) и (13) находим

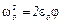. (14)

Пусть n – полное число оборотов, которое делает маятник до остановки, а Т₀ – период вращения маятника в начале движения. Тогда

.

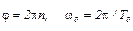и из (14) получаем:

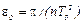. (15)

Отсюда ясно, как на опыте определить ε₀: нужно измерить время Т₀ за которое совершается первый оборот и полное число n оборотов маятника до остановки. Во всех дальнейших измерениях нужно следить, чтобы выполнялось неравенство ε₀<< ε.