Уравнение волны
Пусть некоторая точка O участвует в гармоническом колебательном движении с амплитудой 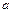 и круговой (циклической) частотой ω. Тогда её смещение от положения равновесия
и круговой (циклической) частотой ω. Тогда её смещение от положения равновесия 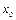 можно описать уравнением:
можно описать уравнением:
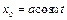 (1)
(1)
Колебания, распространяясь в среде, дойдут до точки A, рис. 2 лежащей на расстоянии r от точки O, через время

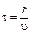 . (2)
. (2)
Скорость υ имеет положительный знак, если направление скорости совпадает с направлением оси r и – отрицательной, если скорость направлена против оси.
Если волна идёт не затухая от точки O в сторону точки A, отстоящей от O на расстояние r, то смещение точки A определяется по формуле (1), но в новый более поздний момент времени 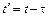 (новая точка придёт в колебание с некоторым запаздыванием на время
(новая точка придёт в колебание с некоторым запаздыванием на время 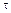 ), тогда
), тогда
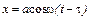
учитывая (2), получим:
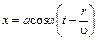 (3)
(3)
Выражение (3) представляет собой уравнение плоской волны, распространяющейся вдоль прямой OA, которое ещё иначе называется уравнением плоской бегущей волны. Оно определяет для любого момента времени t отклонение от положения равновесия колеблющихся частиц 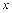 .
.
Учтём известные соотношения
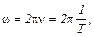
где ν – частота, 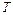 – период колебания.
– период колебания.
И тогда можно записать:
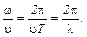
Выражение (3) можно преобразовать к виду:
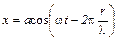
или
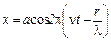 .
.
Звуковые волны могут интерферировать.
Рассмотрим случай интерференции двух волн одинаковой частоты, длины и амплитуды, распространяющихся в противоположных направлениях. На опыте это можно осуществить, если на пути бегущей волны перпендикулярно к направлению распространения поставить хорошо отражающую преграду. В результате интерференции волны падающей и волны отражённой возникает так называемая стоячая волна. Выведем уравнение стоячей волны.
Падающая (бегущая) волна, распространяющаяся по направлению оси r, описывается уравнением:

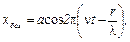
а отражённая
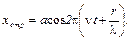
В скобке (–) поменялся на (+) за счет того, что у скорости отражённой волны поменялось направление на противоположное (отражённая волна движется против оси r).
Уравнение стоячей волны получится при сложении уравнений бегущеё и отражённой волн:
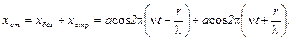
Вынося общий множитель а и используя формулу суммы двух косинусов, находим:
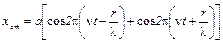
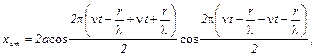
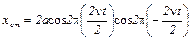 , т.к.
, т.к. 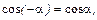
то 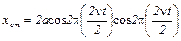 .
.
Уравнение стоячей волны запишется:
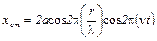 (4)
(4)
В этом уравнении множитель
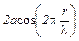 ,
,
не зависящий от времени, выражает результирующую амплитуду A
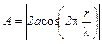 (5)
(5)
Так как функция 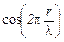 может принимать значения в пределах от нуля до единицы, то точки в стоячей волне, для которых
может принимать значения в пределах от нуля до единицы, то точки в стоячей волне, для которых
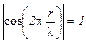 (6)
(6)
будут иметь наибольшую амплитуду: 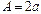 . Такие точки стоячей волны называются пучностями, их координаты определяются из равенства (6)
. Такие точки стоячей волны называются пучностями, их координаты определяются из равенства (6)
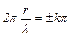 ,
,
откуда
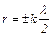 , (7)
, (7)
где 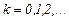
Точки, для которых 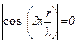 , имеют амплитуду, равную нулю и называются узлами стоячей волны. Их координаты находятся из условия
, имеют амплитуду, равную нулю и называются узлами стоячей волны. Их координаты находятся из условия
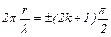 , откуда
, откуда 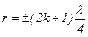 (8)
(8)
Из отношений (7) и (8) следует, что расстояние между соседними узлами (или соседними пучностями) в стоячей волне равно 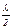 . Из (5) следует, что амплитуда стоячей волны зависит от координаты r колеблющейся точки, т.е. у разных точек среды разные амплитуды, чего в бегущей волне не наблюдается.
. Из (5) следует, что амплитуда стоячей волны зависит от координаты r колеблющейся точки, т.е. у разных точек среды разные амплитуды, чего в бегущей волне не наблюдается.
В уравнении стоячей волны множитель 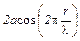 при переходе через нулевое значение меняет знак, в соответствии с этим фаза колебаний по разные стороны от узла отличается на
при переходе через нулевое значение меняет знак, в соответствии с этим фаза колебаний по разные стороны от узла отличается на 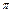 , т.е. точки, лежащие по разные стороны от узла, колеблются в противофазе, а все точки, заключенные между двумя соседними узлами, колеблются синфазно (т.е. в одной и той же фазе).
, т.е. точки, лежащие по разные стороны от узла, колеблются в противофазе, а все точки, заключенные между двумя соседними узлами, колеблются синфазно (т.е. в одной и той же фазе).
На рис. 4 дан ряд моментальных фотографий отклонений точек от положения равновесия. Первая соответствует моменту, когда отклонения достигают наибольшего абсолютного значения. Последующие рисунки сделаны с интервалами в четверть периода.
 Вторая соответствует одновременному прохождению частиц через положение равновесия. Третья фотография соответствует одновременному отклонению частиц, но в другую сторону (стрелками показаны скорости частиц).
Вторая соответствует одновременному прохождению частиц через положение равновесия. Третья фотография соответствует одновременному отклонению частиц, но в другую сторону (стрелками показаны скорости частиц).
Рассмотрим несколько примеров колебаний сплошных систем. В закреплённой с обоих концов натянутой струне при возбуждении поперечных колебаний устанавливаются стоячие волны, причём в местах закрепления струны должны располагаться узлы. Поэтому в струне возбуждаются только такие колебания, половина длины волны которых укладывается на длине струны целое число раз. Отсюда вытекает условие
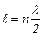 или
или 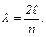 (9)
(9)
где 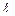 – длина струны, а
– длина струны, а 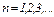

Подобным образом можно рассматривать собственные колебания столба воздуха, заключённого в трубе с открытыми концами. В этом случае на концах образуется пучности стоячей волны, т.к. отражаясь от менее плотной среды волна не меняет фазы в месте отражения. Как и в предыдущем случае на всей длине столба воздуха уложится целое число 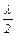
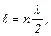 где
где 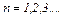
В системе с неодинаковыми условиями отражения волн на концах, например, в воздушном слое трубы, закрытой только у одного конца, также можно возбудить собственные колебания. Стоячие волны в этом случае имеют на открытом конце пучность, а на закрытом – узел стоячей волны. На всей длине столба воздуха 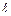 уложится или
уложится или 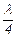 , или
, или 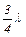 , или
, или 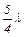 , и т.д., т.е. длины стоячих волн, устанавливающихся в воздушном столбе, открытом с одного конца, должны удовлетворять условию:
, и т.д., т.е. длины стоячих волн, устанавливающихся в воздушном столбе, открытом с одного конца, должны удовлетворять условию:
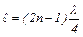 , где
, где 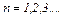 (10)
(10)

Случай возникновения стоячей волны в столбе воздуха используют для нахождения частоты этих колебаний.
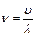 (11)
(11)
Источником звука в данной работе служит звуковой генератор. Для определения длины волны издаваемого генератором звука, пользуются стоячими волнами, образующимися в стеклянной трубке, которая закрыта с одного конца подвижной преградой. Если у открытого конца трубы поместить телефон, соединённый с генератором звука, то колебания его мембраны передаются воздушному столбу в трубке. Воздушный столб будет резонировать только в том случае, если период его собственных колебаний совпадает с периодом колебаний звука, издаваемого генератором (явление резонанса). Звуковая волна от телефона, размещённого у открытого конца трубки, распространяясь по воздуху, дойдёт до преграды, находящейся на втором конце трубки, поменяет фазу на противофазу и пойдёт навстречу бегущей волне. Бегущая и отражённая волны создадут стоячую волну. У поверхности преграды всегда образуется узел, у открытого конца трубки – пучность. В зависимости от высоты воздушного столба, а также от частоты колебаний мембраны в трубке расположится то или иное число узлов и пучностей стоячей волны. Звук мембраны усиливается, когда она оказывается в пучностях стоячей волны. Длина самого короткого воздушного столба, которая резонирует мембране телефона, имеет узел у преграды и пучность у открытого конца трубки; следовательно, длина его равна четверти длины звуковой волны в воздухе. Если трубка достаточно длинная, то резонанс в трубке может повториться, когда высота столба воздуха будет равна трём, пяти или другому нечётному числу четвертей длины звуковой волны в воздухе. Необходимо заметить, что у открытого конца трубки всегда имеется некоторое смещение пучностей. Чтобы учесть его, при измерении вводят так называемую поправку на открытый конец, которая не зависит от длины волны и равна приблизительно 0,6R, где R – радиус трубки. Если 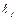 – длина первого, самого короткого столба воздуха, дающего резонанс;
– длина первого, самого короткого столба воздуха, дающего резонанс; 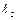 – длина второго, то
– длина второго, то
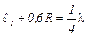
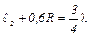
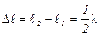
Отсюда 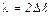 . Подставив это выражение в (10), получим рабочую формулу:
. Подставив это выражение в (10), получим рабочую формулу:
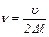 ,
,
где 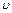 – скорость звука при данной температуре
– скорость звука при данной температуре 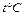 . Для определения скорости звука при данной температуре t пользуются формулой
. Для определения скорости звука при данной температуре t пользуются формулой
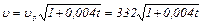
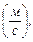
где 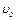 = 332
= 332 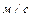 – скорость звука при
– скорость звука при 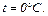
Подставив это в рабочую
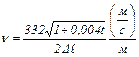 (12)
(12)
1 вариант работы
Дата добавления: 2015-10-05; просмотров: 820;
