Соответствие, отображения и функции

Соответствие – соответствием между множествами А и В называется подмножество GÍА х В. Соответствие G называется функциональным или однозначным, если образом любого элемента множества G₁ является единственный элемент множества G₂, причем G₁, G₂Í G.

Пример. Англо-русский словарь устанавливает соответствие между множеством английских и русских слов. Это соответствие не является функциональным.

Функцией называется функциональное соответствие. Если функция f устанавливает соответствие между множествами А и В, то говорят, что функция f имеет тип А®В (обозначение f : А®В). Полностью определенная функция f : А®В называется отображением А в В. Образ А при отображении f обозначается f(A).

Если f(A) состоит из единственного элемента, то f называется функцией –константа.

Отображение типа А®А называется преобразованием множества А.

Важным понятием при построении математических моделей дискретной математики является понятие отношения между элементами двух множеств. Если для каждого элемента x Î X можно сказать, что элемент x находится либо не находится в данном отношении a с элементом y Î Y, то говорят, что между элементами множества X и Y задано отношение a, и пишут x a y, в том случае, когда x находится в отношении с элементом y. Например, между множеством Х студентов данного курса и множеством Y всех учебных предметов по данной специальности существует отношение a такое, что х a y означает «студент х сдал экзамен по предмету y. Между элементами множеств Х и Y может существовать много различных содержательных отношений, если Х и Y - содержательные множества. Например, такими отношениями являются всевозможные функциональныеотношения, или отображения.

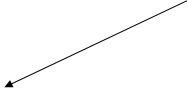
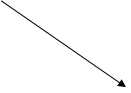
Отображения. Отношения a между элементами множеств X и Y называют отображениеммножества Х в множество Y, если каждый элемент х Î Х обязательно находиться в отношении с некоторым элементом y Î Y, причем этот элемент y Î Y - единственный для данного элемента х Î Х. Отображение множества Х в множество Y обозначают через j (либо другой подходящей буквой) и пишут j: Х ® Y, при этом вместо х j y для х Î Х и y Î Y часто пишут y = j(х) и говорят что y есть образ элемента х при отображении. На картинке отображение j : Х ® Y удобно представлять в виде двудольного графа.

х₁ х₂ х₃ х₄

X

j

Y

у₁ у₂ у₃ у₄

Здесь точки верхнего ряда изображают элементы множества Х, нижнего ряда - множества Y, и если имеет место y = j(x), то из точки х выходит стрелка, заходящая или входящая в точку y. Такую картинку называют двудольным графом отображения j: X ® Y, причем точки этой картинки именуют вершинами графа, а стрелки - дугами графа и говорят, что отображение j является :

а). Инъективным, если в каждую вершину y Î Y заходит или входит не более одной дуги ;

б). Сюръективным, если в каждую вершину y Î Y входит не менее одной дуги ;

в). Биективным, или биекцией, если j инъективно и сюръективно одновременно.

Для любого отображения j : X ® Y и любого не пустого подмножества А Í Х множество образов всех элементов х Î А при отображении j называют образом множества А и обозначают j(А),так что j(А) = íy ÎY : y = j(x) для некоторого х Î Аý.

Для общности и стройности суждений полагают j(Æ) = Æ. Если j(Х) = Y, то, очевидно, j является сюръективным отображением.

В приложениях часто используется отображение j: Х ® R⁺, при этом j(х) выступает в роли цены, или веса, или длины, или пропускной способности элемента х Î Х.

Очевидно, задание биекции j: X ® Y равносильны установлению взаимно однозначного соответствия между элементами множеств Х и Y.

Отображения j: Х ® Y и Y₁: Х ® Y называются равными, если из х j y следует x j₁ y и наоборот, т.е. если эти отображения можно изобразить одним и тем же двудольным графом отображения.

Пусть Х и Y - конечные непустые множества, причем |X| = m, |Y| = n. Тогда количество всех отображений j: X ® Y равно n^m. Действительно, чтобы получить произвольное отображение j X ® Y, надо построить двудольный граф этого отображения, для чего выбрать для каждой вершины x Î X одну и только одну дугу среди n дуг (n = |Y| ), которые могут выходить из вершины х и заходить в вершины y Î Y, причем для разных вершин х, х₁Î Х указанный выбор дуг делается независимо. Поэтому количество всех таких выборов, а значит, и всех двудольных графов отображений будет n*n*...*n, где количество сомножителей равно m = |X|, так что получается искомое количество n^m.

Множество всех отображений j: X ® Y иногда обозначают как Y^x, ибо для конечных X и Y тогда получают формулу |Y^x| = |Y^|x||. Но никто и нечто не мешает рассматривать последнюю формулу для бесконечных X и Y и считать эту формулу правилом возведения в кардинальную степень |X| кардинального числа |Y|.

Например, с = 2^a . Далее, сумму |X| + |Y| произвольных кардинальных чисел определяют как мощность |X + Y| множества X + Y, составленного из всех вершин х Î Х и y Î Y двудольного графа произвольного отображения j: X ® Y, а произведение |X| * |Y| определяют как мощность |X * Y| множества X * Y, составленного из всевозможных упорядоченных пар (x, y), где x Î X, y Î Y, т.е. из дуг двудольного графа, в котором из каждой вершины x Î X выходят дуги в каждую вершину y ÎY. Такое определение суммы и произведения кардинальных чисел согласуется с обычным смыслом m + n и m * n для конечных множеств X и Y при m = =|X|, n = |Y|.

Преобразования. Отображение j:X ® X называют преобразованием множества Х и на картинке изображают в виде орграфа (ориентированного графа) преобразования, вершинами которого являются элементы x Î X, а дугами - пары (х₁, х₂) такие, что х₁j х₂ , т.е. х₂ = j(х₁). Преобразования j: X ® X можно изображать двустрочной записью, помещая в первой строке этой записи элементы x Î X, а во второй - под ними их образы j(х). Например, для

Х = í1,2,...,7ý одно из преобразований изобразим двустрочной записью и орграфом :

1 2 3 4 5 6 7 3

j =

3 7 2 5 4 6 1 1 2 4 5 6

7

Видно, что это преобразование биективно, причем j(А) = А для множеств А=Æ, А = í1,2,3,7ý А = í4,5ý ,А = í6ý, и только для них.

Биективные преобразования называют подстановками. Очевидно орграф подстановки j конечного множества распадается на части, однозначно определяемые подмножествами А такими, что А = j(А). Такие части (вершины вместе с дугами ) принято называть циклами подстановки j. Максимальное количество циклов имеет тождественная подстановка j, т.е. такая, что х = j(х) выполняемая для любого х Î Х. Подстановки, имеющие один цикл, называются одноцикловыми. Одноцикловые подстановки служат, например, моделями для описания обхода одним человеком n различных пунктов (начав движение в исходном пункте, человек обходит все остальные по одному разу и возвращается в исходный пункт). Заметим, что количество всех подстановок n -элементного множества Х равно n! = n * (n-1)*...*2*1, потому что элементу x₁ Î X можно поставить в соответствие любой из n элементов множества Х, но элементу х₂ при х₂ ¹ х₁, можно поставить в соответствие по подстановке j любой элемент из оставшихся n-1 элементов, которые не являются образом элемента х₁ и т.д.

В связи со сказанным выше удобно обозначить через Х! множество всех бииективных преобразований множества Х, ибо тогда | X! | = | X |! для конечных множеств Х.

Рекомендуется помнить, что 10! = 3628800, а 0! = 1 (по соглашению).

Разумеется, количество всех одноцикловых подстановок n - элементного множества равно (n-1)!.

Пример 1. Каждое натуральное число можно разложить на произведение простых чисел. Если расположить простые делители в определенном порядке например не убывание то получим функцию

G(42)=(2, 3, 7); G(23)=23;

G(100)=(2, 2, 5, 5) и т. д.

Пример 2. Каждому человеку соответствует множество его знакомых.

G(Иванов)=(Сидоров, Николаев,…..,Семенов)

Способы задания функций.

Наиболее простой способ задания функций – это таблица, т. е. список пар (x, f(x)). Однако таким образом могут задаваться только функции, определенные на конечном множестве. Таблицы функций, определенных на бесконечных множествах (например, тригонометрических) задают эти функции только в конечном числе точек.

Другим способом задания функций является формула, описывающая функцию, как суперпозицию других (исходных) функций. Для задания функции могут использоваться также графики

Еще два способа задания функций:

а) рекурсивная процедура

б) ì x, если xÎM

f(x) = í

î 0, если xÏM

Упражнения.

1. Найдите множества АÇВ, АÈВ, А\В, В\А, если:

а) А={3,5,6,7,9}, В={4,6,7,8};

б) А={3,5,6,7,9}, В={2,4,8};

в) А={2,3,4,5,6}, В={3,4,5};

г) А=Z, В=N; д) А=R, В=Q,; е) А=Z, В=Q;

ж) А={x|xÎR, -1£x£5},В={x|xÎR, -3£x£2};

з) А={x|xÎR, -1£x£3}, В={x|xÎR,3£x5};

и) А-множество всех прямоугольников, В- множество всех ромбов.

2. Найдите множества Аи В если:

а) А\В={a,b},В\А={c,d},АÇВ={x,y,z};

б) АÈВ={a,b,c,d,e,f},АÇВ={c,d},А\В={a,e,f};

в) АÈВ={a,b,c,d}, АÇВ=Æ, А\В={a}.

3. Пусть А - множество решений уравнений f(x)=0, В - множество решений уравнения п(ч)=0 .Выразите через А и В множество решений:

а) уравнения f(x)g(x)=0;

б) уравнения f(x)g(x)=0;

f(x)=0;

в) системы уравнений

g(x)=0.

4. Выразите множество действительных корней уравнения f(x)=0

через множества А={x|f(x)>0}и В={x|f(x)<0}.

5. Найдите следующие множества:

а) АÈÆ; б) АÇÆ; в) АÈА; г)АÇА;

д) А\А; е) А\Æ; ж) Æ/А.

6. Даны множества А и В , причем АÌВ. Найдите:

а) АÈВ; б) АÇВ; в)А\В.

7. На диаграмме Эйлера-Венна изображены множества А,В,С(рис.8). Укажите (заштрихуйте)на этой диаграмме множества:

а) АÇВ(ВÈС); б) АÇ(ВÇС);

в) (А\В)ÇС;

г) (А\В)È(В\С).

8. Докажите, что для любых множеств А,В,С:

а) АÇ(ВÈС)=(АÇВ)È(АÇС);

б) АÈ(ВÇС)=(АÈВ)Ç(АÈС);

в) А\(ВÇС)=(А\В)È(А\С).

9. Пусть А и В - подмножества множества М. Докажите, что :

а) `АÈ`В=АÇВ; б) `АÇ`В= АÈВ.

10. Множество А состоит из n элементов , а множество В- из m элементов (m>n)/ какое наибольшее и наименьшее число элементов могут содержать множества АÈВ, АÇВ, А\В, В\А?

11. докажите, что если А состоит из n элементов, В- из m элементов, АÇВ - из k элементов, то множество АÈВ состоит из n+m-k элементов.

12. Каждый ученик в классе изучает английский или французкий язык. Английский язык изучают 25 человек, французкий-27, а оба языка-18. Сколько учеников в классе ?

13. В классе 30 учеников. Каждый из них занимается футболом, либо хоккеем. Половина учеников класса занимается хоккеем, а 5 учеников -и хоккеем и футболом. Сколько учеников в классе занимается футболом ?