Коэффициенты множественной корреляции и детерминации

Общее качество уравнения множественной регрессии оценивается с помощью коэффициента множественной корреляции и его квадрата – коэффициента множественной детерминации.

По аналогии с парной регрессией коэффициент множественной детерминацииможно определить как долю дисперсии результата, объясненную вариацией включенных в модель факторов, в его общей дисперсии:

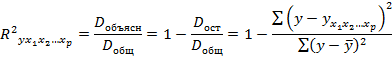
Значения коэффициента множественной детерминации изменяются от нуля до единицы (0≤R²_yx1x2…xp≤1). Чем ближе этот коэффициент к единице, тем больше уравнение регрессии объясняет поведение результата.

Коэффициент множественной корреляциихарактеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или, иными словами, оценивает тесноту связи совместного влияния факторов на результат.

Коэффициент множественной корреляции может быть найден как корень квадратный из коэффициента множественной детерминации:

Значения коэффициентов множественной корреляции изменяются от нуля до единицы (0≤R_yx1x2…xp≤1). Чем ближе коэффициент единице, тем теснее связь между результатом и всеми факторами в совокупности и уравнение регрессии лучше описывает фактические данные. Если множественный коэффициент корреляции R_yx1x2…xp близок к нулю, то уравнение регрессии плохо описывает фактические данные, и факторы оказывают слабое влияние на результат.

Значение коэффициента множественной корреляции больше или равно величине максимального коэффициента парной корреляции:

R_{y x1x2…xp} ≥ І r_{y xi (max)} І , где i = 1,р.

Если в уравнении регрессии учитывается какой-либо фактор, оказывающий наиболее сильное воздействие на результативный признак, то частный коэффициент корреляции будет достаточно близок к коэффициенту множественной корреляции, но ни в коем случае не больше него.

Иногда для расчета коэффициента множественной корреляции используется еще одна формула (она применима только для линейной множественной регрессии):

где DetІR⁺І, DetІRІ - определители матриц соответственно парных коэффициентов корреляции и межфакторной корреляции.

Эти определители будут иметь следующий вид для уравнения линейной множественной регрессии с р числом факторов:

1 r_yx1 r_yx2 … r_yxp

r_yx1 1 r_x1x2 … r_x1xp

Det ІR⁺І = r_yx2 r_x1x2 1 … r_x2xp ,

… … … … …

r_yxp r_x1xp r_x2xp … 1

т.е. матрица включает все парные коэффициенты корреляции для уравнения регрессии;

1 r_x1x2 … r_x1xp

Det ІRІ = r_x1x2 1 … r_x2xp

… … … … ,

r_x1xp r_x2xp … 1

т.е. данная матрица получается из предыдущей матрицы путем исключения коэффициентов парной корреляции факторов с результатом (вычеркиваются первая строка и первый столбец).

Для того, чтобы не допустить возможного преувеличения тесноты связи, обычно применяется скорректированный коэффициент множественной корреляции. Он содержит поправку на число степеней свободы. Ocтaточная сумма квадратов отклонений делится на число степеней свободы остаточной вариации (п - т - 1), а общая сумма квадратов отклонений - на число степеней свободы в целом по совокупности (п - 1). Формула скорректированного коэффициента множественной корреляции имеет следующий вид:

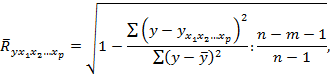
где т - число параметров при переменных х (в линейной зависимости оно будет равно числу включаемых в модель факторов = p); п - число наблюдений.

Так как 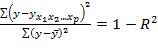, R² – коэффициент множественной детерминации, то скорректированный коэффициент множественной корреляции

а скорректированный коэффициент множественной детерминации

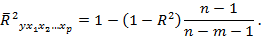
Добавление в модель новых объясняющих переменных осуществляется до тех пор, пока растет скорректированный коэффициент детерминации.