Метод последовательных разностей.
В ряде случаев вместо аналитического выравнивания с целью устранения тенденции можно применить метод последовательных разностей.
Если временной ряд содержит линейную тенденцию, её можно устранить путём замены исходных уровней ряда цепными приростами (первыми разностями). Если временной ряд содержит тенденцию в форме параболы второго порядка, то для её устранения можно заменить исходные уровни ряда на вторые разности.
Пример. Изучение зависимости по первым разностям предыдущего примера.
Составим таблицу.
| Время | 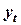
| 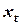
| 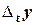
| 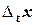
|
| 78,86 | 8,09 | - | - | |
| 83,19 | 8,88 | 4,33 | 0,7875 | |
| 83,18 | 8,91 | -0,01 | 0,0375 | |
| 79,7 | 9,00 | -3,48 | 0,0875 | |
| 76,67 | 9,29 | -3,03 | 0,2875 | |
| 76,54 | 9,28 | -0,13 | -0,0125 | |
| 73,94 | 9,91 | -2,6 | 0,6375 | |
| 72,23 | 10,00 | -1,71 | 0,0875 | |
| 67,91 | 10,09 | -4,32 | 0,0875 | |
| 66,56 | 10,08 | -1,35 | -0,0125 | |
| 62,85 | 10,31 | -3,71 | 0,2375 | |
| 59,78 | 11,00 | -3,07 | 0,6875 | |
| 56,96 | 11,09 | -2,82 | 0,0875 | |
| 49,92 | 11,08 | -7,04 | -0,0125 | |
| 46,21 | 10,91 | -3,71 | -0,1625 | |
| 37,36 | 10,80 | -8,85 | -0,1125 |
Коэффициенты автокорреляции первого порядка для первых разностей составят: 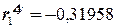 и
и  . Найдем уравнение регрессии по первым разностям
. Найдем уравнение регрессии по первым разностям  . Коэффициент детерминации составит
. Коэффициент детерминации составит 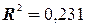 .
.
В отличие от уравнения регрессии по отклонениям от тренда, параметрам данного уравнения легко дать интерпретацию. При изменении прироста дохода на 1 д. е. прирост потребления изменяется в среднем на 0,49 д. е. в ту же сторону. При всей своей простоте метод последовательных разностей имеет два существенных недостатка. Во-первых, его применение связано с сокращением числа пар наблюдений, по которым строится уравнение регрессии, и, следовательно, с потерей числа степеней свободы. Во-вторых, использование вместо исходных уровней временных рядов их приростов или ускорений приводит к потере информации, содержащейся в исходных данных.
Дата добавления: 2015-10-05; просмотров: 1710;
