Геометрическая вероятность для одномерного случая

Одним из недостатков классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным количеством исходов. В таких случаях можно воспользоваться понятием геометрической вероятности.

Пусть на отрезок L наудачу брошена точка. Это означает, что точка обязательно попадет на отрезок L и с равной возможностью может совпасть с любой точкой этого отрезка. При этом вероятность попадания точки на любую часть отрезка L не зависит от расположения этой части на отрезке и пропорциональна его длине. Тогда вероятность того, что брошенная точка попадет на отрезок l, являющийся частью отрезка L, вычисляется по формуле:

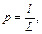(1)

где l – длина отрезка l, а L – длина отрезка L.

Можно дать аналогичную постановку задачи для точки, брошенной на плоскую область S и вероятности того, что она попадет на часть этой области s:

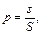(2)

где s – площадь части области, а S – площадь всей области.

В трехмерном случае вероятность того, что точка, случайным образом расположенная в теле V, попадет в его часть v, задается формулой:

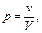(3)

где v – объем части тела, а V – объем всего тела.

Пример 1. Найти вероятность того, что точка, наудачу брошенная в круг, не попадет в правильный шестиугольник, вписанный в него.

Решение. Пусть радиус круга равен R , тогда сторона шестиугольника тоже равна R. При этом площадь круга 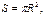а площадь шестиугольника 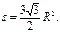Следовательно,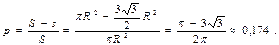

Пример 2. На отрезок АВ случайным образом брошены три точки: С, D и М. Найти вероятность того, что из отрезков АС, АD и АМ можно построить треугольник.

Решение. Обозначим длины отрезков АС, АD и АМ через x, y и z и рассмотрим в качестве возможных исходов множество точек трехмерного пространства с координатами (х, у, z). Если принять длину отрезка равной 1, то эти множество возможных исходов представляет собой куб с ребром, равным 1. Тогда множество благоприятных исходов состоит из точек, для координат которых выполнены неравенства треугольника: x + y > z, x + z > y, y + z > x. Это часть куба, отрезанная от него плоскостями x + y = z, x + z = y, y + z =х

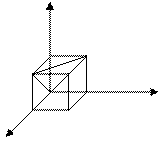
Рисунок 1 – плоскость x + y = z

(одна из них, плоскость x + y = z, проведена на рис.1). Каждая такая плоскость отделяет от куба пирамиду, объем которой равен 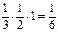. Следовательно, объем оставшейся части 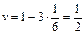. Тогда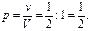

Задание для самостоятельной работы:

Подобрать одно задание на применение геометрической вероятности и изобразить графически. Оформить согласно требований.

Рекомендуемая литература: 1;3; 4; 5.