График функции распределения для дискретной случайной величины
Определение: Функцией распределения F(x)случайной величины Х называется вероятность того, что случайная величина примет значение, меньшее х:
F (x) = p (X < x).
Свойства функции распределения:
1)0 ≤ F(x) ≤ 1.
Действительно, так как функция распределения представляет собой вероятность, она может принимать только те значения, которые принимает вероятность.
2)Функция распределения является неубывающей функцией, то есть F(x2) ≥ F(x1) при х2 > x1. Это следует из того, что F(x2) = p(X < x2) = p(X < x1) + p(x1 ≤ X < x2) ≥ F(x1).
3) 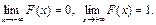 В частности, если все возможные значения Х лежат на интервале [a, b], то F(x) = 0 при х ≤ а и F(x) = 1 при х ≥ b. Действительно, X < a – событие невозможное, а X < b – достоверное.
В частности, если все возможные значения Х лежат на интервале [a, b], то F(x) = 0 при х ≤ а и F(x) = 1 при х ≥ b. Действительно, X < a – событие невозможное, а X < b – достоверное.
4)Вероятность того, что случайная величина примет значение из интервала [a, b], равна разности значений функции распределения на концах интервала: p ( a < X < b ) = F(b) – F(a).
Справедливость этого утверждения следует из определения функции распределения (см. свойство 2).
Для дискретной случайной величины значение F(x) в каждой точке представляет собой сумму вероятностей тех ее возможных значений, которые меньше аргумента функции.
Пример 1. Найдем F(x) по данному закону распределения
| хi | |||
| pi | 0,12 | 0,46 | 0,42 |
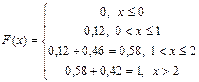
Соответственно график функции распределения имеет ступенчатый вид:
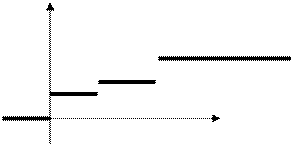 |
Пример 2.По данному закону распределения найти функцию распределения и построить ее график
| х | |||||||||||
| р | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
х<2 F(x)=0
2<=x<3 F(x)=1/36
3<=x<4 F(x)=1/36+2/36=3/36
4<=x<5 F(x)=6/36
5<=x<6 F(x)=10/36
6<=x<7 F(x)=15/36
7<=x<8 F(x)=21/36
8<=x<9 F(x)=25/36
9<=x<10 F(x)=30/36
10<=x<11 F(x)=33/36
11<=x<12 F(x)=1
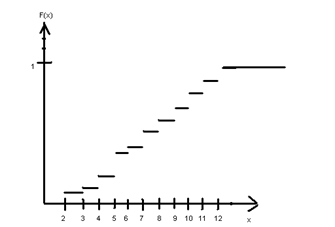
Задание для самостоятельной работы:
Построить график функции распределения предложенного варианта. Оформить согласно требований.
| 1 вариант | ||||||||||||||
| ||||||||||||||
| 2 вариант | ||||||||||||||
| ||||||||||||||
| 3 вариант | ||||||||||||||
| ||||||||||||||
| 4 вариант | ||||||||||||||
| ||||||||||||||
| 5 вариант | ||||||||||||||
| ||||||||||||||
| 6 вариант | ||||||||||||||
| ||||||||||||||
| 7 вариант | ||||||||||||||
| ||||||||||||||
| 8 вариант | ||||||||||||||
| ||||||||||||||
| 9 вариант | ||||||||||||||
| ||||||||||||||
| 10 вариант | ||||||||||||||
|
Рекомендуемая литература: 1;3;4.
Дата добавления: 2015-09-29; просмотров: 1371;
