Теорема Бернулли

Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равно р.

Теорема Бернулли. Если в каждом из п независимых испытаний вероятность р появления события А постоянна, то сколь угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний р достаточно велико.

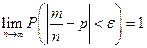
Здесь т – число появлений события А. Из приведённых выше утверждений вообще говоря не следует, что с увеличением число испытаний относительная частота неуклонно стремится к вероятности р, т.е. 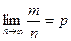. В теореме имеется в виду только вероятность приближения относительной частоты к вероятности появления события А в каждом испытании.

В случае, если вероятности появления события А в каждом опыте различны, то справедлива следующая теорема.

Теорема Пуассона. Если производится п независимых опытов и вероятность появления события А в каждом опыте равна 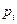, то при увеличении п частота события А сходится по вероятности к среднему арифметическому вероятностей .

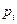Замечание. Сформулированные утверждения остаются в силе и для непрерывных случайных величин.