Теорема Чебышева

Теорема Чебышева. Если 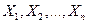- попарно независимые случайные величины, причем дисперсии их равномерно ограничены, то для любого сколь угодно малого положительное число e, вероятность неравенства

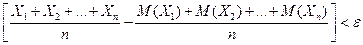
будет сколь угодно близка к единице, если число случайных величин достаточно велико, т.е.справедливо равенство:

.

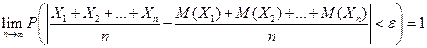Иногда случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева упрощается:

.

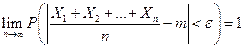Дробь, входящая в записанное выше выражение является средним арифметическим возможных значений случайной величины.

Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий.

Отклоняясь от математического ожидания, как в положительную, так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно сокращаются.

Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности.