Закон больших чисел. Неравенство Чебышева
Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке академика А.Н. Колмогорова, совокупное действие большого числа случайных величин приводит (при некоторых весьма общих условиях) к результаты, почти не зависящему от случая. Другими словами:
Если случайная величина Х представляет собой сумму достаточно большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму бесконечно мало, то Х имеет распределение, близкое к нормальному.
Этот факт имеет очень важное значение на практике, т.к. позволяет предвидеть результат опыта при воздействии большого числа случайных факторов.
Рассмотрим дискретную случайную величину Х, заданную таблицей распределения:
| X | 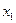
| 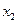
| … | 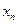
|
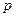
| 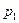
| 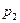
| … | 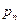
|
Требуется определить вероятность того, что отклонение значения случайной величины от ее математического ожидания будет не больше, чем заданное число 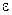 .
.
Теорема. (Неравенство Чебышева) Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине меньше положительного числа e, не меньше чем 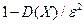 :
:
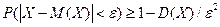 .
.
Дата добавления: 2015-09-29; просмотров: 698;
