Уравнение Бернулли. Определение. Уравнением Бернуллиназывается уравнение вида
Определение. Уравнением Бернуллиназывается уравнение вида
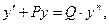
где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.
Для решения уравнения Бернулли применяют подстановку 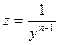 , с помощью которой, уравнение Бернулли приводится к линейному.
, с помощью которой, уравнение Бернулли приводится к линейному.
Исходное уравнение делят на 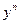 :
:
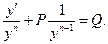
Используем подстановку, учитывая, что 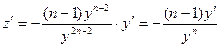 . Находим
. Находим
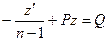 ;
; 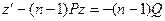 .
.
Получаем линейное уравнение относительно неизвестной функции z.
Решение этого уравнения будем искать в виде:
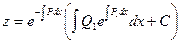 , где
, где

Пример. Решить уравнение 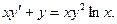
Разделим уравнение на 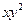 :
: 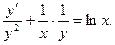
Полагаем 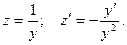 Находим:
Находим:
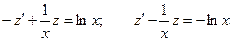 .
.
Полагая 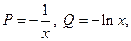 будем иметь:
будем иметь:
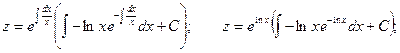
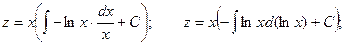
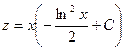 .
.
Произведя обратную подстановку, получаем:
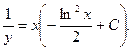
Пример. Решить уравнение 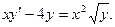
Разделим обе части уравнения на 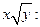
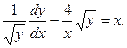
Полагаем 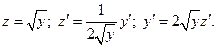 Находим:
Находим:
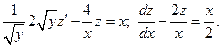
Получили линейное неоднородное дифференциальное уравнение. Рассмотрим соответствующее ему линейное однородное уравнение:
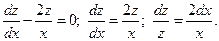
Интегрируя обе части, получаем:
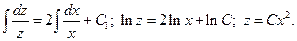
Полагая 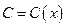 , подставляем полученный результат в линейное неоднородное уравнение, учитывая, что
, подставляем полученный результат в линейное неоднородное уравнение, учитывая, что
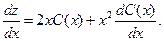
Находим:
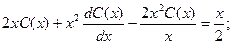
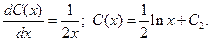
Получаем: 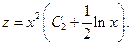 Применяя обратную подстановку, получаем окончательный ответ:
Применяя обратную подстановку, получаем окончательный ответ:
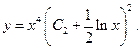
Дата добавления: 2015-09-29; просмотров: 533;
