Непрерывность функции нескольких переменных по отдельным переменным

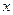Зафиксируем переменную , а переменной придадим произвольное приращение 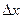. Функция 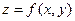получит приращение:

,

которое называется частным приращением функции в точке 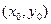, соответствующим приращению 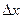аргумента 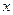. Заметим, что 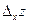является функцией одной переменной 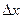. Аналогично,

.

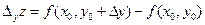Определение. Функция 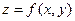называется непрерывной в точке 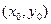по переменной 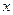(по переменной 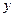), если

.

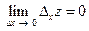
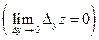В отличие от непрерывности по отдельным переменным обычную непрерывность функции называют иногда непрерывностью по совокупности переменных.

Теорема. Если функция 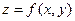определена в некоторой окрестности точки 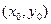и непрерывна в этой точке, то она непрерывна в этой точке по каждой из переменных.

Обратное утверждение вообще говоря неверно.

Пример. Докажем, что функция

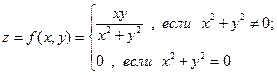
непрерывна в точке 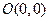по каждой переменно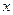й и 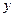, но не является непрерывной в этой точке по совокупности переменных.

Рассмотрим частное приращение функции 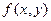в точке 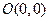, соответствующее приращению 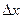аргумента :

.

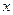Очевидно, что , а это означает, что 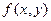непрерывна в точке 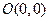по переменной .

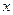Аналогично доказывается, что функция 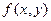непрерывна в точке 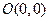по переменной .

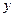Покажем, что предел 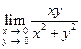не существует. Пусть точка 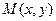стремиться к точке 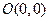по прямой 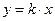, проходящей через точку 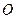. Тогда получим

.

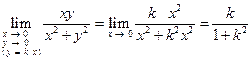Таким образом, приближаясь к точке 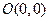по различным прямым, соответствующим разным значениям , получаем разные предельные значения. Отсюда следует, что предел данной функции в точке 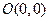не существует, а значит, функция 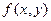не является непрерывной в этой точке.