Предел функции нескольких переменных

Определение. Говорят, что последовательность точек 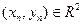сходится при 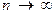к точке 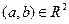, если 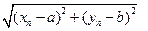стремится к 0 при 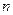стремящемся к 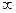. В этом случае точку 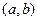называют пределом указанной последовательности и пишут: 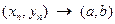при .

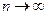Можно показать, что 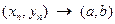при 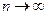тогда и только тогда, когда одновременно числовая последовательность 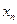сходится к числу 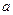, а числовая последовательность 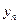сходится к числу 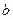при 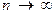(т.е. сходимость последовательности точек пространства 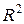эквивалентна покоординатной сходимости).

Пусть 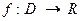и 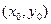– предельная точка множества .

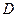Определение. Число 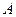называют пределом функци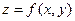и при 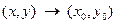, если для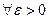 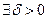такое, что 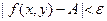, как только 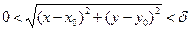. В этом случае пишут

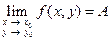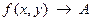или при .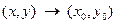

Замечание.В случае функции одной переменной для существования предела в точке необходимо и достаточно равенство лишь двух чисел – пределов по двум направлениям: справа и слева от предельной точки 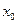. Для функции двух переменных стремление к предельной точке 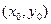на плоскости 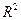может происходить по бесконечному числу направлений (и необязательно по прямой).

Пример. Найти .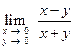

Пусть стремление к предельной точке 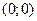происходит по прямой 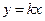. Тогда

.

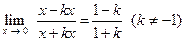Предел, очевидно, не существует, так как число 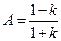зависит от .

Пример. Найти .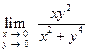

По любой прямой 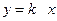предел один и тот же:

.

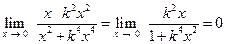С другой стороны, пусть стремление к предельной точке происходит по кривой 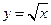. Тогда

.

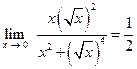Следовательно, предела не существует.

Сформулируем понятие предела функции для случая, её аргументы стремятся к к бесконечности. Ограничимся случаем, когда 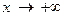, 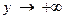(понятие предела функции в остальных случаях формулируются аналогично).

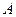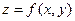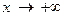Определение. Число называют пределом функции при и 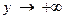, если для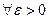 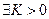такое, что из неравенств 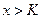и 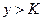следует неравенство 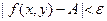. Этот факт коротко записывают так:

.

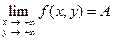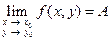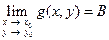Теорема. Если существуют и , то

;

;

,

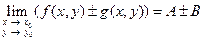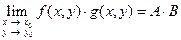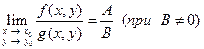где предельная точка 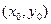может быть конечной или бесконечной.

Справедливы аналоги и других теорем о свойствах пределов функций одной переменной.