ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ МЕТОДОМ НАГРЕТОЙ НИТИ

Известны три способа передачи теплоты: теплопроводность, конвекция и лучеиспускание. Только при конвекции и теплопроводности в передаче теплоты участвует газ. Конвекция обусловлена разностью плотностей нагретых и холодных слоев газа: в поле тяготения более нагретые слои поднимаются вверх, а более холодные опускаются вниз.

Если в соседних слоях газа создана и поддерживается разная температура, то между ними будет происходить обмен тепла. Средняя энергия молекул газа, пропорциональная абсолютной температуре 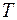, в обоих слоях будет различной. Благодаря хаотическому движению, молекулы в обоих слоях будут перемешиваться, и средние энергии, а, следовательно, и температуры слоев будут выравниваться. При этом будет наблюдаться перенос энергии от более нагретых к более холодным слоям. Этот процесс носит название теплопроводности.

Опыт показывает, что количество теплоты, переносимое в газе через некоторую площадку при теплопроводности будет тем больше, чем больше площадка , чем больше промежуток времени 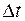, за который наблюдается перенос тепла, и чем быстрее происходит изменение температуры 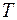в направлении оси 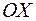, перпендикулярной к площадке , т.е. чем выше градиент температуры 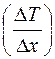(рис. 2.1):

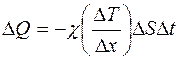. (2.1)

Коэффициент пропорциональности 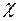называется коэффициентом теплопроводности.

Отношение количества теплоты 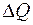, проходящего через площадку за время 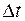, ко времени 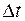называется тепловым потоком:

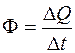. (2.2)

Отношение теплового потока 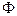, проходящего через площадку , к величине называется удельным тепловым потоком :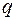

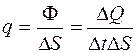. (2.3)

Из уравнений (2.1) – (2.3) получаем:

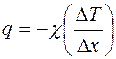. (2.4)

Знак минус означает, что тепло переносится в сторону убывания температуры.

Уравнение (2.4) называется законом Фурье для теплопроводности: удельный тепловой поток при теплопроводности прямо пропорционален градиенту температуры.

Из уравнения (2.4) следует физический смысл коэффициента теплопроводности: коэффициент теплопроводности численно равен удельному тепловому потоку при единичном градиенте температуры.

Уравнение (2.4) описывает стационарный процесс теплопроводности, при котором разность температур между горячим и холодным слоями со временем не изменяется и градиент температуры в каждой точке тоже не меняется со временем.

Рассмотрим стационарный процесс теплопроводности с точки зрения молекулярно-кинетической теории газов.

Согласно молекулярно – кинетической теории, перенос количества теплоты 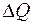через площадку (рис. 2.1) означает перенос определенного количества кинетической энергии беспорядочно движущихся молекул.

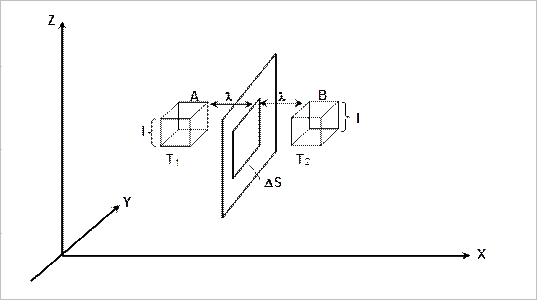
Рис. 2.1. Перенос молекулами энергии

Примем, что температура 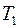больше, чем 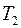. Введем в рассмотрение два кубика 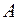и 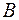, расположенные слева и справа от площадки на расстояниях, равных средней длине свободного пробега 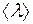. Через площадку проходят молекулы как слева направо, так и справа налево. Если давление газа во всех точках одно и тоже, то число молекул 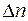, пересекающих в единицу времени площадку слева и справа, одинаково (см. лабораторную работу 1) и равно:

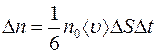. (2.5)

Все молекулы, подошедшие к слева обладают средней кинетической энергией

,

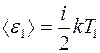где 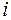- число степеней свободы молекулы.

Эти молекулы переносят через площадку количество энергии равное

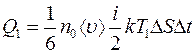. (2.6)

Аналогично этому: количество энергии, переносимое молекулами, подходящими к площадке справа

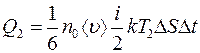. (2.7)

В результате через площадку будет перенесено тепло:

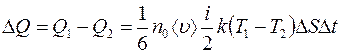. (2.8)

Разность температур 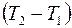между точками, находящимися по обе стороны от площадки на расстоянии от нее, можно представить так:

.

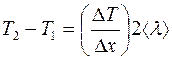Отсюда:

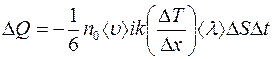. (2.9)

Сравнивая это значение 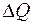со значением (2.1), для коэффициента теплопроводности найдем:

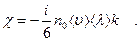(2.10)

Величину 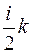преобразуем следующим образом:

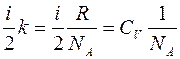, (2.11)

где 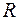– универсальная газовая постоянная; 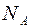– число Авогадро; а 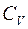–молярная теплоемкость газа при постоянном объеме.

Тогда

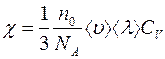(2.12)

или

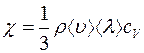, (2.13)

где 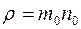( 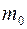– масса одной молекулы газа) – плотность газа; 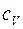– удельная теплоемкость при постоянном объеме.

Из входящих в соотношение (2.13) величин число молекул в единице объема 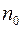и средняя длина свободного пробега 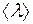зависят от давления. Но первая из них пропорциональна, а вторая – обратно пропорциональна давлению газа. Следовательно, коэффициент теплопроводности 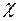от давления не зависит. Этот вывод находится в полном согласии с опытными данными.

Из выражения (2.13) следует, что коэффициент теплопроводности, зависящий от средней скорости теплового движения молекул 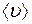, должен меняться с изменением температуры как 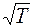. В действительности, коэффициент теплопроводности растет несколько быстрее, чем 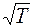. Этот экспериментальный факт можно объяснить тем, что коэффициент теплопроводности пропорционален 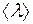, которая тоже растет с температурой.

Возрастание 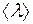с температурой связано с тем, что молекулы газа нельзя рассматривать как твердые шарики. В самом деле, из молекулярно-кинетической теории следует, что средняя длина свободного пробега 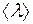, равна:

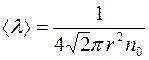(2.14)

и не зависит от температуры ( 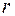– эффективный радиус молекулы). Опыт показывает, что такая зависимость, хотя и слабая, существует: с повышением температуры длина свободного пробега растет. Это объясняется тем, что 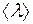обратно пропорциональна поперечному сечению молекулы 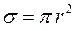. Поперечное сечение молекулы 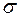определяется тем расстоянием, на которое сближаются молекулы при столкновениях, т.е. расстоянием, на котором сила взаимодействия между молекулами вызывает уже заметное изменение направления их движения.

Поперечное сечение молекул должно, таким образом, зависеть от их скорости (энергии), так как при одной и той же силе взаимодействия быстрые молекулы испытывают меньшее отклонения от своего пути, чем более медленные молекулы. Поэтому, чем больше скорость молекул, тем меньше должно быть расстояние между ними при столкновении. Следовательно, с увеличением скорости молекул, т.е. с повышением температуры газа, поперечное сечение молекул уменьшается, а длина свободного пробега растет.