Методика эксперимента. Экспериментальное изучение теплопроводности газов затрудняется тем, что перенос тепла в газе может происходить не только при теплопроводности
Экспериментальное изучение теплопроводности газов затрудняется тем, что перенос тепла в газе может происходить не только при теплопроводности, но и при конвекции, легко возникающей в газе. Конвекция, так же как и теплопроводность, стремится выровнять температуры в газе, поэтому отличить на опыте эти два механизма теплопередачи затруднительно, и при измерении теплопроводности необходимо обеспечить такие условия, при которых конвекция не может возникнуть.
Один из наиболее распространенных методов измерения коэффициента теплопроводности газов состоит в следующем.
Исследуемым газом заполняют пространство между двумя коаксиальными цилиндрами с радиусами 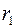 и
и 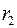 (рис. 2.2), один из которых (почти всегда – внутренний) нагревается электрической печью, потребляющей мощность
(рис. 2.2), один из которых (почти всегда – внутренний) нагревается электрической печью, потребляющей мощность 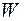 , а другой охлаждается так, чтобы его температура
, а другой охлаждается так, чтобы его температура 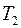 оставалась все время постоянной. Внутренним цилиндром, в частности, может быть тонкая металлическая нить, по которой пропускается электрический ток, так что она же служит и нагревателем.
оставалась все время постоянной. Внутренним цилиндром, в частности, может быть тонкая металлическая нить, по которой пропускается электрический ток, так что она же служит и нагревателем.
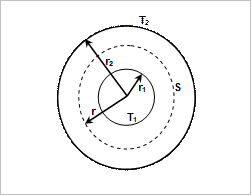
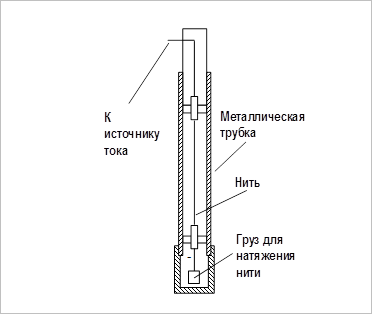
Рис. 2.2. Принципиальная схема установки
для определения коэффициента теплопроводности в газах
Через некоторое время после включения нагревателя устанавливается стационарное состояние, при котором температура 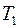 нити тоже становится постоянной.
нити тоже становится постоянной.
Тем самым между внешним цилиндром и нитью установится постоянная разность температур 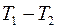 . Величина этой разности температур зависит от теплопроводности газа. Найдем эту зависимость.
. Величина этой разности температур зависит от теплопроводности газа. Найдем эту зависимость.
Если высота цилиндра равна 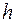 (во избежание ошибки, связанной с конвекцией, прибор следует устанавливать вертикально), тепловой поток
(во избежание ошибки, связанной с конвекцией, прибор следует устанавливать вертикально), тепловой поток 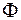 через любое цилиндрическое сечение
через любое цилиндрическое сечение 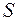 радиуса
радиуса 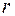 определяется уравнением:
определяется уравнением:
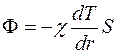 ,
,
где 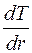 – градиент температуры4
– градиент температуры4 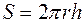 . Если высота цилиндра достаточно велика по сравнению с его радиусом, то температуру вдоль оси цилиндра можно считать всюду одинаковой.
. Если высота цилиндра достаточно велика по сравнению с его радиусом, то температуру вдоль оси цилиндра можно считать всюду одинаковой.
В стационарном состоянии 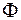 равно мощности нагревателя
равно мощности нагревателя 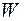 . Следовательно,
. Следовательно,
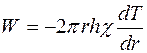 ,
,
откуда
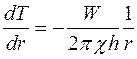 или
или
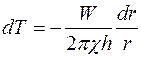 .
.
Интегрируя последнее уравнение, получаем:
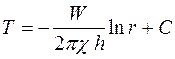 ,
,
где 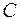 – постоянная интегрирования, которую можно исключить, принимая во внимание, что температура
– постоянная интегрирования, которую можно исключить, принимая во внимание, что температура 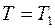 при
при 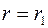 и
и 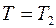 при
при 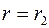 , т.е.
, т.е.
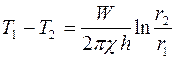 . (2.15)
. (2.15)
Измерив температуры 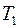 и
и 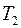 , зная геометрические размеры прибора и мощность нагревателя, можно вычислить коэффициент теплопроводности:
, зная геометрические размеры прибора и мощность нагревателя, можно вычислить коэффициент теплопроводности:
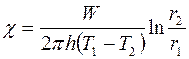 . (2.16)
. (2.16)
Мощность нагревателя 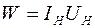 , где
, где 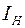 и
и 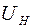 – сила тока и падение напряжения на нити.
– сила тока и падение напряжения на нити.
Температура трубки 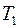 во время эксперимента остается постоянной и равной комнатной, т.к. ее поверхность обдувается с помощью вентилятора потоком воздуха.
во время эксперимента остается постоянной и равной комнатной, т.к. ее поверхность обдувается с помощью вентилятора потоком воздуха.
Для определения температуры нити 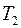 находят ее сопротивление в нагретом состоянии, используя известную зависимость сопротивления от температуры:
находят ее сопротивление в нагретом состоянии, используя известную зависимость сопротивления от температуры:
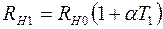 ; (2.17)
; (2.17)
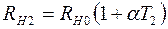 , (2.18)
, (2.18)
где 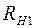 ,
, 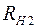 – сопротивления нити при температурах
– сопротивления нити при температурах 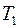 и
и 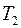 соответственно;
соответственно; 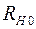 – сопротивление нити при
– сопротивление нити при 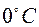 ;
; 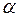 – температурный коэффициент сопротивления нити.
– температурный коэффициент сопротивления нити.
Из соотношений (2.17) и (2.18) выразим температуру 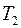 :
:
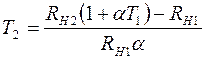 . (2.19)
. (2.19)
Следовательно, разность температур нити и стенок трубки 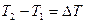 равна:
равна:
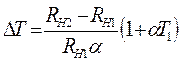 . (2.20)
. (2.20)
Для определения сопротивления нити при комнатной температуре и в нагретом состоянии, последовательно с ней включают эталонный резистор с сопротивлением 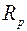 . Тогда токи, текущие по нити и через эталонный резистор оказываются одинаковыми:
. Тогда токи, текущие по нити и через эталонный резистор оказываются одинаковыми:
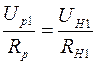 и
и 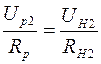 , (2.21)
, (2.21)
где 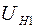 ,
, 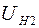 – падения напряжений на нити при температурах
– падения напряжений на нити при температурах 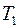 и
и 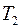 ;
; 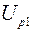 ,
, 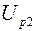 – соответствующие падения напряжений на эталонном резисторе.
– соответствующие падения напряжений на эталонном резисторе.
Используя соотношения (2.21) для разности температур, получаем
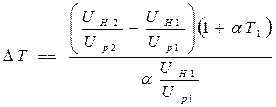 . (2.22)
. (2.22)
Мощность нагревателя 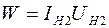 с учетом соотношения (2.21) можно представить в виде:
с учетом соотношения (2.21) можно представить в виде:
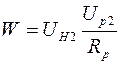 . (2.23)
. (2.23)
Подставляя (2.22) и (2.23) в выражение (2.16) для коэффициента теплопроводности, получим:
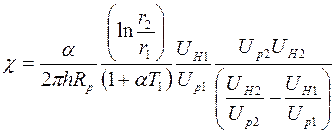 . (2.24)
. (2.24)
Соотношение (2.24) представляет собой рабочую формулу для вычисления коэффициента теплопроводности 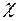 .
.
Дата добавления: 2015-09-29; просмотров: 961;
