Типы уравнений и способы их решения

Всюду далее f(x), g(x), h(x) – некоторые выражения с переменной (число).

I тип: уравнение вида

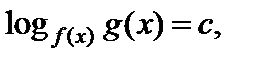(6.8)

где c Î R.

ОДЗ: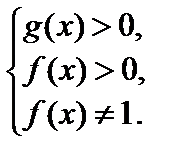

На указанной ОДЗ уравнение (6.8) решают по определению логарифма:

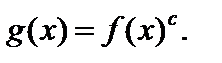
II тип: уравнение вида

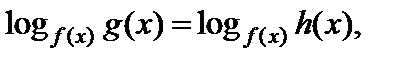(6.9)

ОДЗ: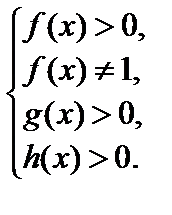

На основании равенства логарифмов, уравнение (6.9) сводится к равносильному ему (на указанной ОДЗ) уравнению:

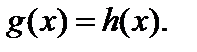
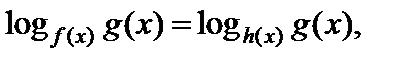(6.10)

ОДЗ: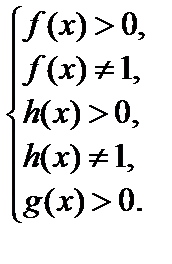

Данное уравнение на ОДЗ равносильно совокупности уравнений:

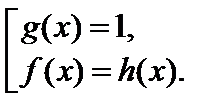
III тип: уравнения, решаемые заменой переменной

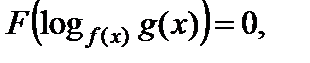(6.11)

где F – некоторое выражение относительно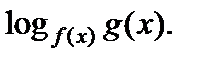

Необходимо определить ОДЗ уравнения, учитывая все условия существования логарифма и выражения F.

Далее заменяют 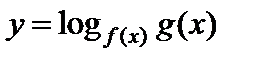и решают уравнение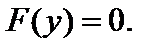

Если 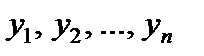– корни последнего уравнения, то, после возвращения к старой переменной, необходимо решить совокупность

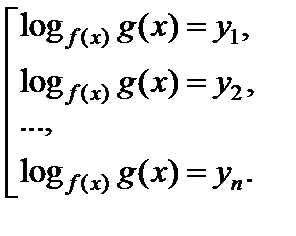
Полученные корни проверяют по ОДЗ.

З а м е ч а н и е. Если вместо какого-либо выражения f(x), g(x), h(x) уравнения (6.8)–(6.11) содержат число, то соответствующее условие не записывают в ОДЗ.

Пример 1. Решить уравнение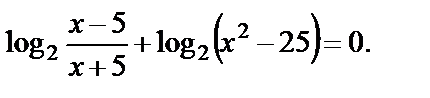

Решение. Находим ОДЗ:

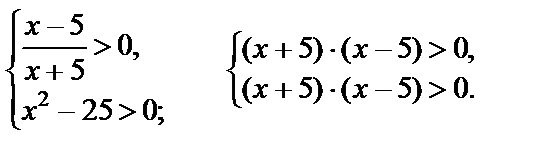
Решение системы:

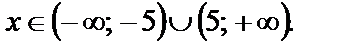
Преобразуем уравнение к виду

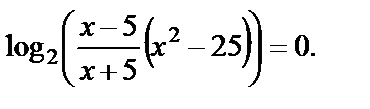
Получили уравнение I типа, которое решается по определению логарифма:

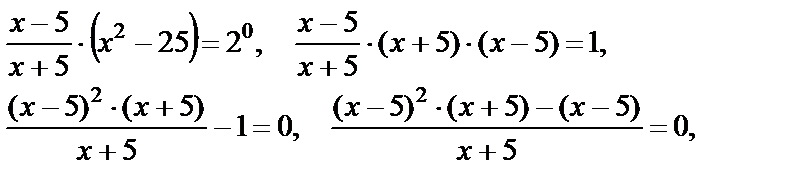
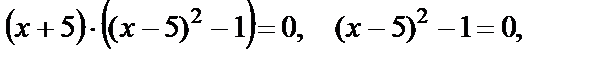
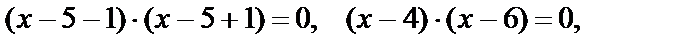
откуда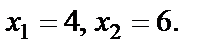

Из полученных значений корень х = 4 не подходит по ОДЗ.

Получаем ответ: х = 6.

Пример 2. Решить уравнение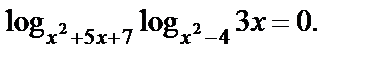

Решение.Записываем условия, определяющие ОДЗ:

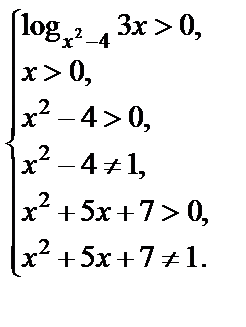
Заданное уравнение относится к I типу. Получаем:

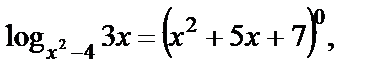
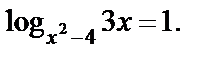
Снова используем определение логарифма:

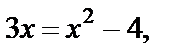т. е. 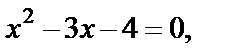откуда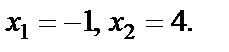

Полученные корни проверяем подстановкой в условия, определяющие ОДЗ уравнения. Убеждаемся, что корень 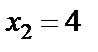подходит, а корень 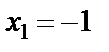не подходит по ОДЗ.

Получаем ответ: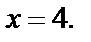

Пример 3. Решить уравнение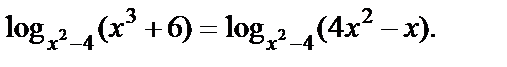

Решение. Записываем условия, определяющие ОДЗ:

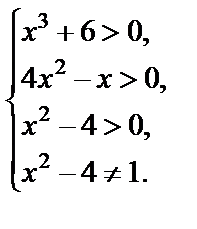
Данное уравнение относится ко II типу, т. е. решается по свойству равенства логарифмов. Получаем:

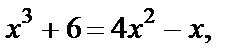т. е.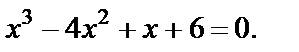

Раскладываем левую часть на множители:

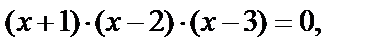откуда получаем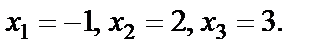

Подставляем найденные значения в ОДЗ, находим, что уравнение имеет только один корень х = 3.

В ответе имеем: х = 3.

Пример 4. Решить уравнение

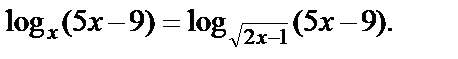
Решение. Находим ОДЗ:

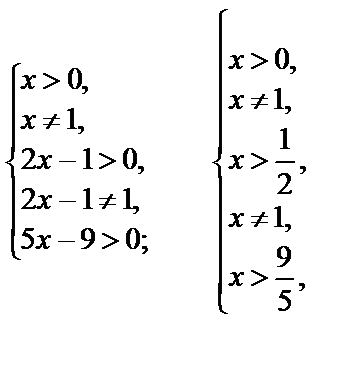т. е.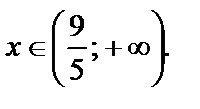

Данное уравнение относится ко II типу. Решаем совокупность:

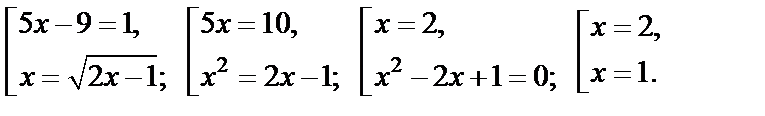
По ОДЗ подходит только корень х = 2, так как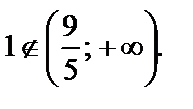

Получаем ответ: х = 2.

Пример 5. Решить уравнение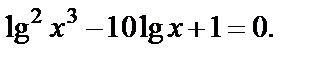

Решение. ОДЗ: 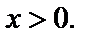Преобразуем уравнение:

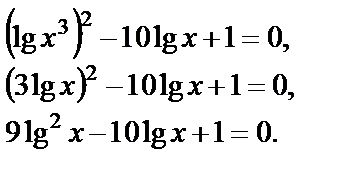
Имеем квадратное уравнение относительно 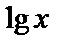(уравнение III типа). Заменяем

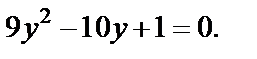
Решая полученное квадратное уравнение, находим корни 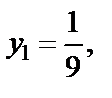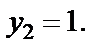Возвращаемся к переменной x:

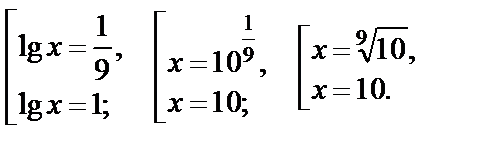
Оба корня подходят по ОДЗ, получаем ответ: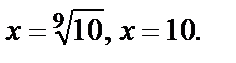

Пример 6.Решить уравнение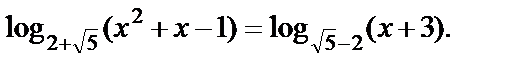

Решение. Запишем условия ОДЗ: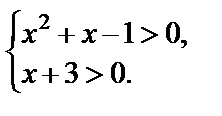

Воспользуемся тем, что

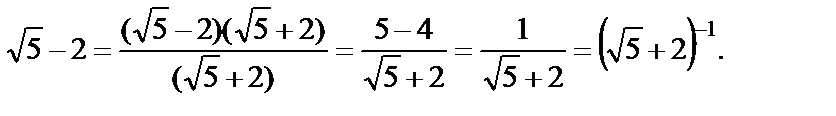Тогда

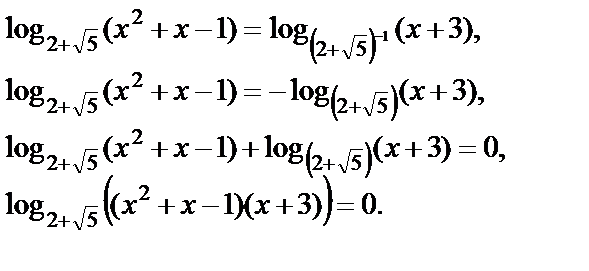
Решаем полученное уравнение как уравнение I типа:

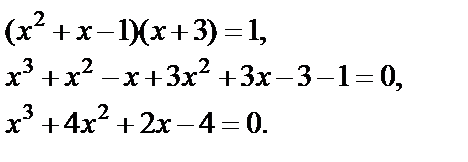
Среди целых делителей свободного члена находим корень х = –2. Он подходит по ОДЗ.

Пришли к ответу: х = –2.

Пример 7. Решить уравнение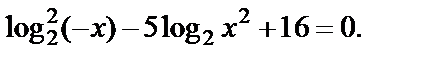

Решение. ОДЗ: 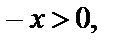т. е.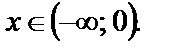

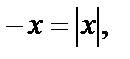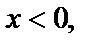Воспользуемся свойствами модуля: если и 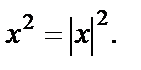Тогда уравнение перепишется в виде

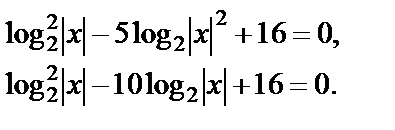
Заменяем 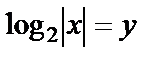и приходим к квадратному уравнению

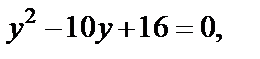
корнями которого являются числа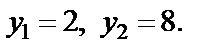

Возвращаемся к старой переменной:

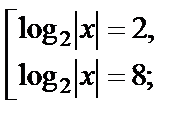
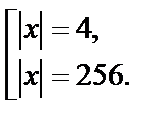
Раскрываем модуль, используя ОДЗ:

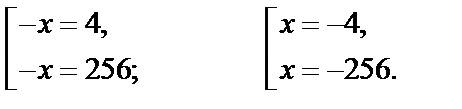
Получаем ответ: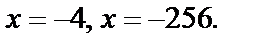

Пример 8. Решить уравнение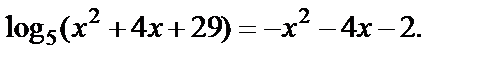

Решение. ОДЗ: 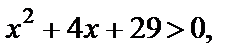т. е. х Î R.

Рассмотрим левую часть уравнения:

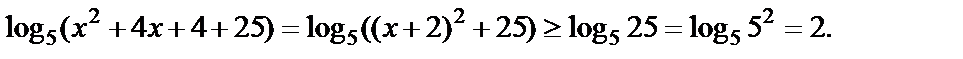
Преобразуем правую часть. Получим:

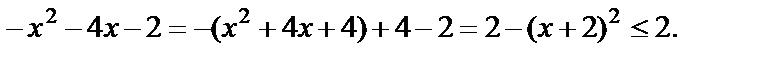
Используя функциональный метод решения, заключаем, что решением исходного уравнения является решение системы

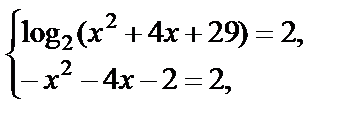т. е. х = –2.

Получаем ответ: х = –2.

Пример 9. Найти сумму корней уравнения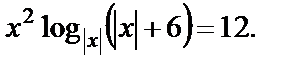

Решение. Для данного уравнения характерно следующее: если х – корень уравнения, то и (–х) тоже корень уравнения. Поэтому если уравнение имеет корни, то их сумма будет равна нулю. Подстановкой находим корни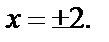

Получаем ответ: 0.