Свойства логарифмической функции
1.Область определения: 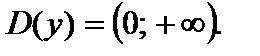
2.Множество значений: 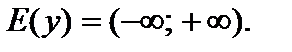
3.Четность и нечетность: функция не обладает свойством четности.
4.Периодичность функции: непериодическая.
5.Нули: функция обращается в нуль при x = 1.
6.Промежутки знакопостоянства: если 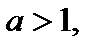 то функция положительна для
то функция положительна для 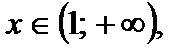 отрицательна для
отрицательна для 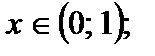 если
если 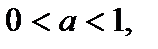 то функция положительна для
то функция положительна для 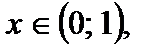 отрицательна для
отрицательна для 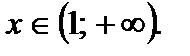
7.Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.
8.Промежутки возрастания и убывания: если 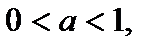 функция убывает для
функция убывает для 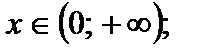 если
если 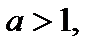 возрастает для
возрастает для 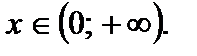
9.Асимптоты: прямая x = 0 (ось Oy) – вертикальная асимптота.
10.График функции для 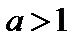 изображен на рис. 6.9, а для
изображен на рис. 6.9, а для 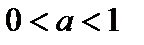 на рис. 6.10.
на рис. 6.10.
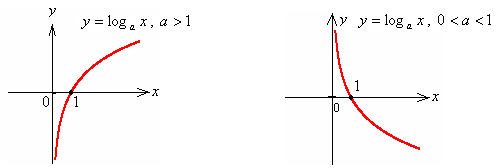
Рис. 6.9 Рис. 6.10
Из свойств функции следует: 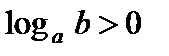 тогда и только тогда, когда
тогда и только тогда, когда
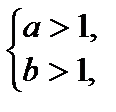 или
или 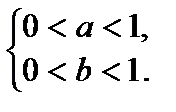
Функция 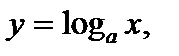 если
если 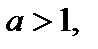 является обратной для функции
является обратной для функции 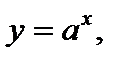 при
при 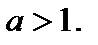
Функция 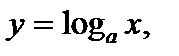 если
если 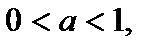 является обратной для функции
является обратной для функции 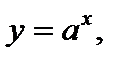 при
при 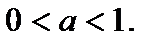
Пример 1. Определить знак числа:
1) 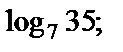 2)
2) 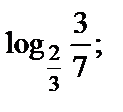 3)
3) 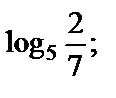 4)
4) 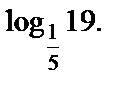
Решение. 1) Поскольку основание логарифма больше 1 (а = 7) и значение, стоящее под знаком логарифма, больше 1 (b = 35), то из свойств логарифмической функции 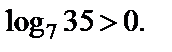
2) Для основания логарифма имеем 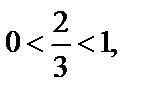 и для выражения, стоящего под знаком логарифма, выполняется
и для выражения, стоящего под знаком логарифма, выполняется 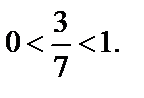 Поэтому
Поэтому 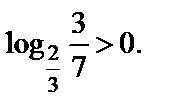
3) Так как основание логарифма 5 и 5 > 1, а выражение, стоящее под знаком логарифма, равно 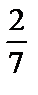 и
и 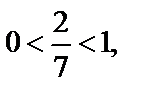 то
то 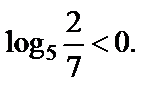
4) Для основания логарифма выполняется 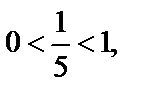 а под знаком логарифма число 19 (19 > 1). Поэтому
а под знаком логарифма число 19 (19 > 1). Поэтому 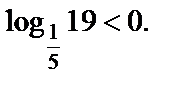
Пример 2. Сравнить числа:
1) 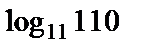 и
и 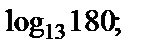 2)
2) 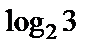 и
и 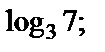
3) 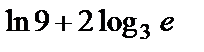 и 3.
и 3.
Решение. 1) Используем тот факт, что логарифмические функции с основанием 11 и 13 монотонно возрастают. Поэтому
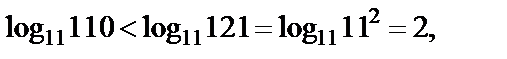
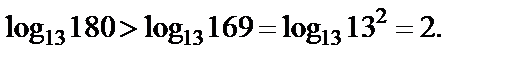
Тогда
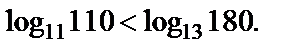
2) Рассмотрим числа 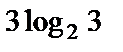 и
и 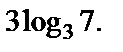 Так как
Так как
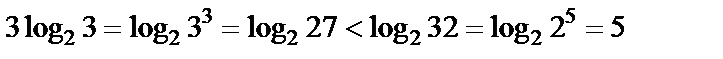 и
и
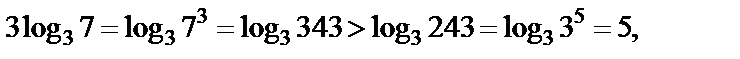 то
то
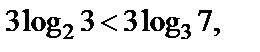 следовательно,
следовательно, 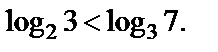
3) Известно, что 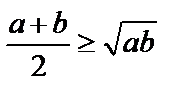 или
или 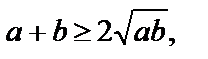
если a ³ 0, b ³ 0.
В нашем случае 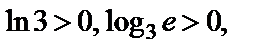 тогда
тогда
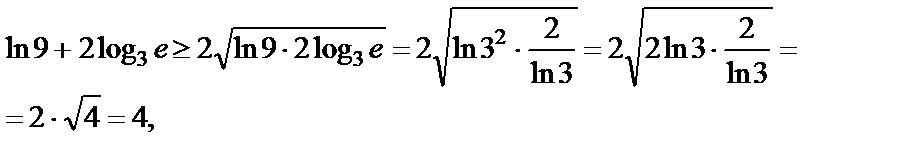
т. е. 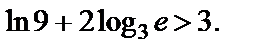
Пример 3. Установить, между какими последовательными целыми числами находится число 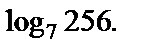
Решение. Поскольку логарифмическая функция с основанием 7 монотонно возрастает, то
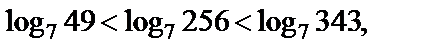
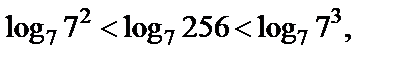
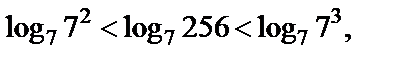
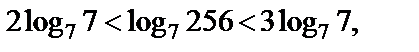
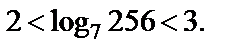
Пример 4. Найти функцию, обратную функции 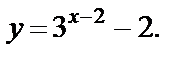 Построить графики обеих функций в одной системе координат.
Построить графики обеих функций в одной системе координат.
Решение. Найдем функцию, обратную данной:
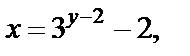
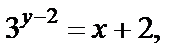
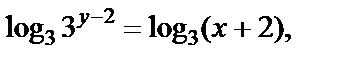
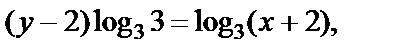
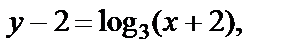
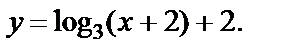
Построим графики функций:
а) строим график функции 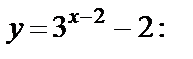 график функции
график функции 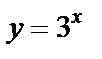 переносим параллельно на две единицы вправо по оси Ox и на две единицы вниз по оси Oy;
переносим параллельно на две единицы вправо по оси Ox и на две единицы вниз по оси Oy;
б) график обратной функции 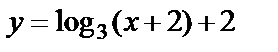 симметричен графику данной функции относительно прямой
симметричен графику данной функции относительно прямой 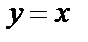 (рис. 6.11).
(рис. 6.11).
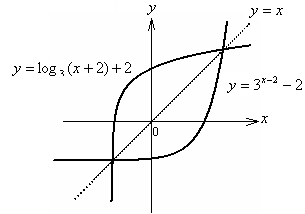
| y = log3(x + 2) + 2 |
| y |
| x |
| y = x |
| y = 3x – 2 – 2 |
Рис. 6.11
Показательные уравнения,
Дата добавления: 2015-09-29; просмотров: 827;
