Типы показательных уравнений и способы их решения

Всюду далее f(x), g(x) – некоторые выражения с неизвестной величиной x.

I тип: уравнение вида

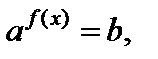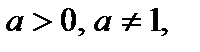где (6.2)

имеет решение, если b > 0. Его решают логарифмированием по основанию a:

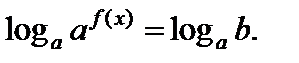
Тогда

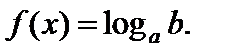(6.3)

Решение уравнения (6.3) производят соответственно типу этого уравнения.

II тип: уравнение вида

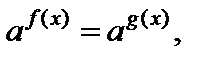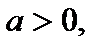где (6.4)

по свойству равенства степеней равносильно уравнению

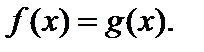
Последнее уравнение решают в зависимости от его типа.

III тип: уравнение вида

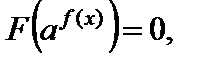(6.5)

где F – некоторое выражение относительно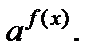

Производят замену переменной 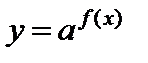и решают уравнение F(y) = 0.

Если 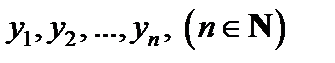– корни уравнения, то после возвращения к старой переменной решение уравнения (6.5) сводится к решению равносильной ему совокупности уравнений

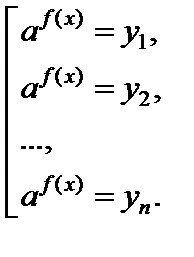
IV тип: уравнения, решаемые графическим методом.

Для таких уравнений строят соответствующие графики для левой и правой частей уравнения. Определяют, для каких значений x графики имеют общую ординату. Используют также иные функциональные свойства, в частности, монотонность функции (возрастание, убывание).

Показательно-степенным уравнением называется уравнение, в котором неизвестная величина содержится и в основании степени, и в показателе. Такие уравнения принято решать при условии, что основания степени положительны (ОДЗ уравнения).