Свойства корней
Пусть a, b ÎR, тогда:
1) 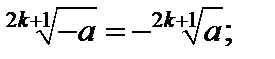
2) 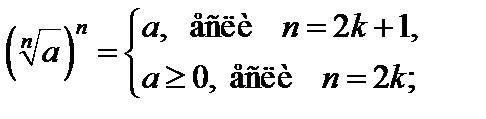
3) 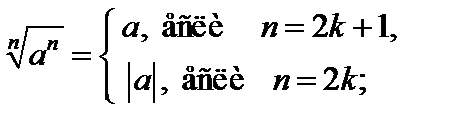
4) 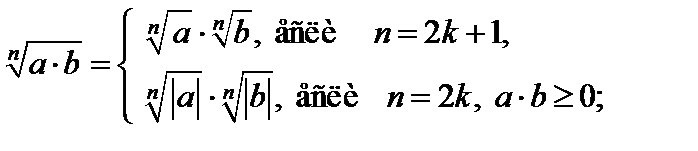
5) 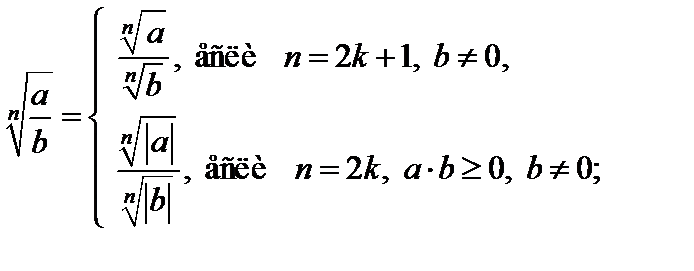
6) 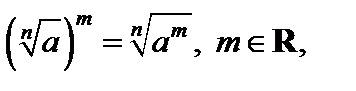 где a ³ 0 в случае
где a ³ 0 в случае 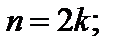
7) 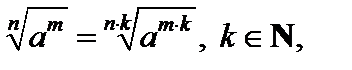 где
где 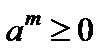 в случае
в случае 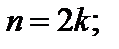
8) 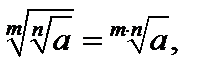 где
где 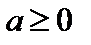 в случае
в случае 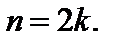
Пример 1.Вычислить 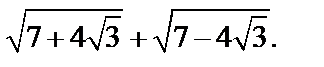
Решение. 1-й способ. Выделим полные квадраты подкоренных выражений:
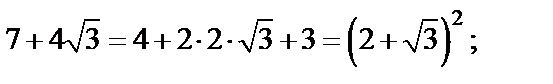
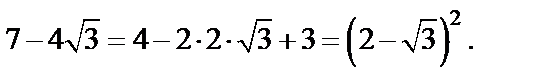
Тогда получим
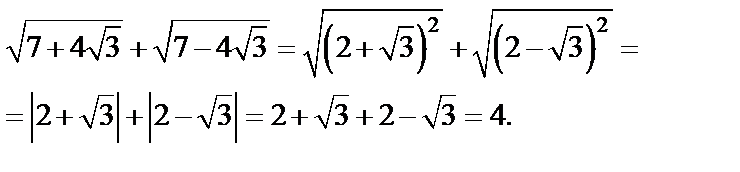
2-й способ. Обозначим вычисляемое выражение через a, т. е.
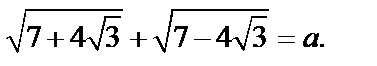 Заметим, что
Заметим, что 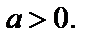
Возведем обе части полученного равенства в квадрат:
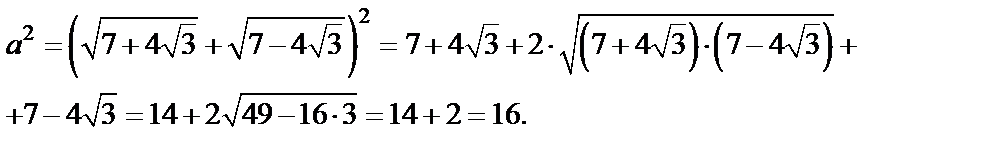
Тогда 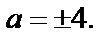
Поскольку исходное выражение положительно, в ответе получаем a = 4.
Пример 2. Упростить выражение 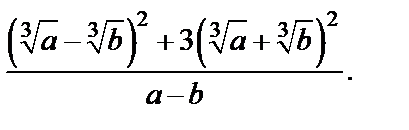
Решение. 1-й способ. Используем формулы квадрата разности и суммы, а также свойства корней. Получаем:
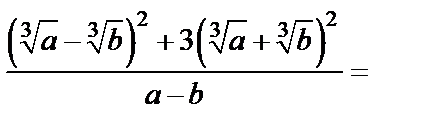
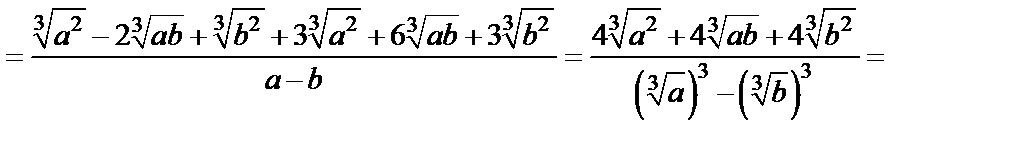
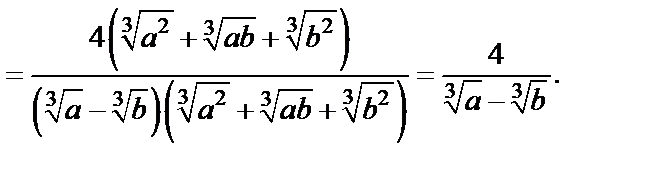
2-й способ. При упрощении иррациональных выражений часто бывает эффективным метод рационализации, основанный на замене переменных.
Введем такую замену переменных, чтобы корни извлеклись: 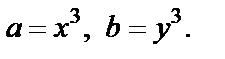
Заданное выражение приобретает вид
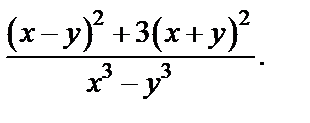
Упрощаем его, используя формулы сокращенного умножения:
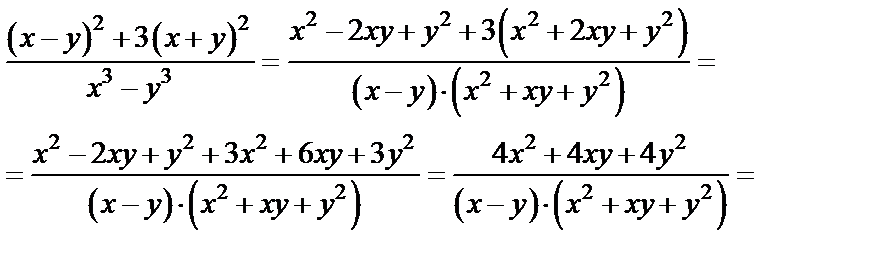
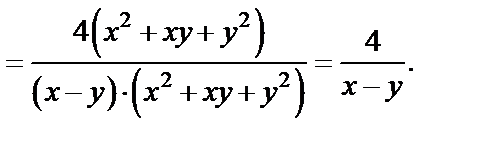
Возвращаясь к старым переменным, приходим к ответу 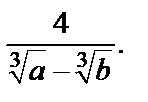
Пример 3. Избавиться от иррациональности в знаменателе:
1) 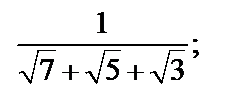 2)
2) 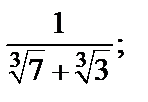 3)
3) 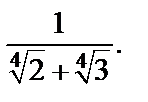
Решение. 1) Умножим числитель и знаменатель дважды на сопряженные выражения и воспользуемся формулой разности квадратов:
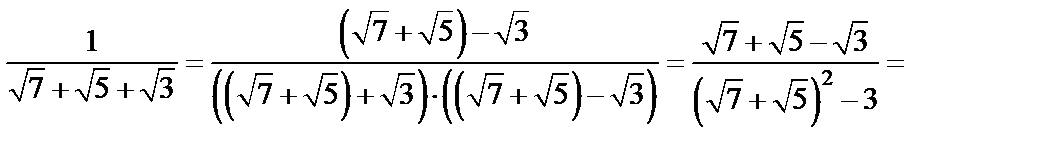
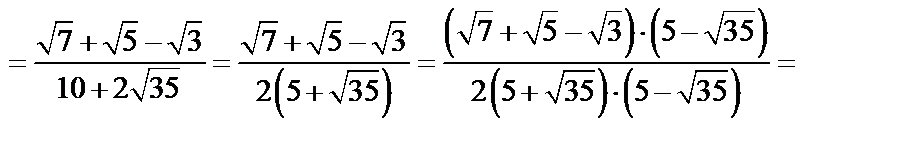
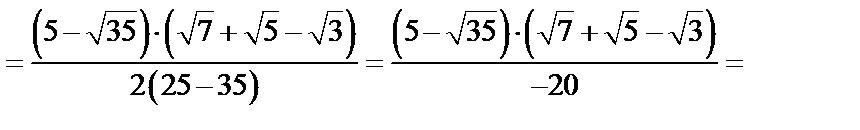
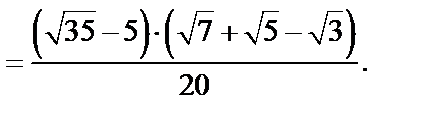
2) Домножим числитель и знаменатель на неполный квадрат разности и воспользуемся формулой суммы кубов:
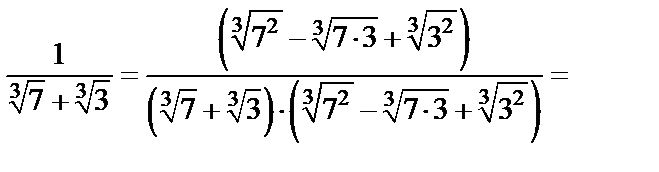
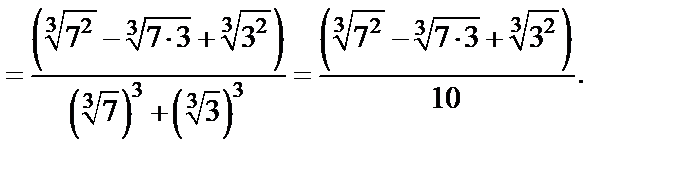
3) Умножим числитель и знаменатель дважды на сопряженные выражения:
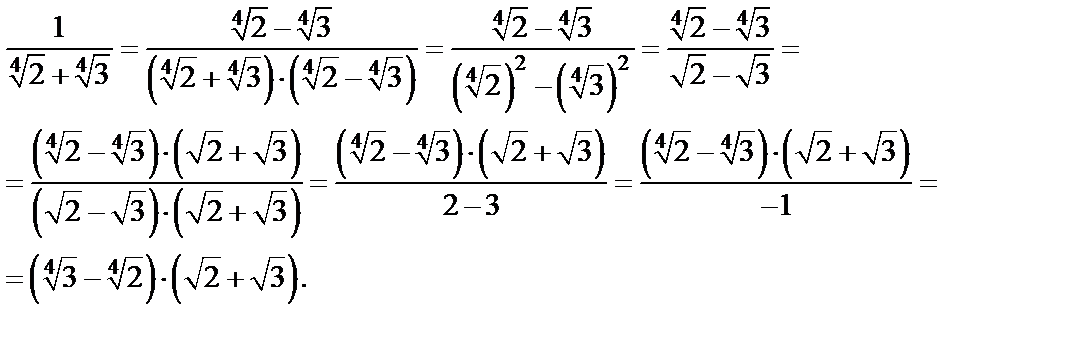
Дата добавления: 2015-09-29; просмотров: 956;
