Преобразования графиков
Приведем графики некоторых функций:
1) 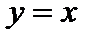 – прямая линия (рис. 4.7); – прямая линия (рис. 4.7);
| 2) 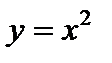 – квадратичная
парабола (рис. 4.8); – квадратичная
парабола (рис. 4.8);
|
| y |
| х |
| y = x |
| y |
| х |
Рис. 4.7 Рис. 4.8
3) 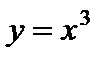 – кубическая парабола (рис. 4.9); – кубическая парабола (рис. 4.9);
| 4) 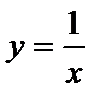 – гипербола
(рис. 4.10); – гипербола
(рис. 4.10);
|
| y |
| x |
| y = x3 |
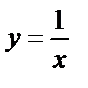
|
| y |
| x |
Рис. 4.9 Рис. 4.10
5) 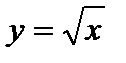 – график квадратного корня (рис. 4.11).
– график квадратного корня (рис. 4.11).
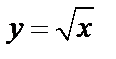
|
| y |
| x |
Рис. 4.11
Правила преобразования графиков:
Пусть дана функция 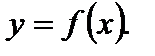
1. Для построения графика функции 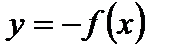 исходный график функции
исходный график функции 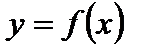 симметрично отображаем относительно оси Ох (рис. 4.12).
симметрично отображаем относительно оси Ох (рис. 4.12).
2. Для функции 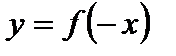 заданный график симметрично отображаем относительно оси Оу (рис. 4.13).
заданный график симметрично отображаем относительно оси Оу (рис. 4.13).
| y |
| x |
| y = f(x) |
| y = –f(x) |
| y |
| x |
| y = f(x) |
| y = f(–x) |
Рис. 4.12 Рис. 4.13
3. Для функции 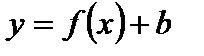 этот график получается параллельным переносом графика функции
этот график получается параллельным переносом графика функции 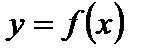 на
на 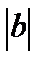 масштабных единиц вдоль оси Оу вверх, если
масштабных единиц вдоль оси Оу вверх, если 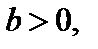 и вниз, если
и вниз, если 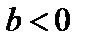 (рис. 4.14).
(рис. 4.14).
4. Для функции 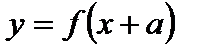 этот график получается параллельным переносом графика функции
этот график получается параллельным переносом графика функции 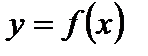 на
на 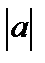 масштабных единиц вдоль оси Ох вправо, если
масштабных единиц вдоль оси Ох вправо, если 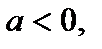 и влево, если
и влево, если 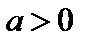 (рис. 4.15).
(рис. 4.15).
| y |
| x |
| y = f(x) + b, b > 0 |
| y = f(x) |
| y = f(x) + b, b < 0 |
| y = f(x) |
| y |
| x |
| y = f(x + a), a > 0 |
| y = f(x + a), a < 0 |
Рис. 4.14 Рис. 4.15
5. Для функции 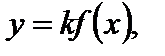 где
где 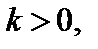 график функции
график функции 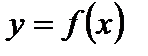 «растянут» в k раз вдоль оси Оу (от оси Ох), если
«растянут» в k раз вдоль оси Оу (от оси Ох), если  «сжат» в
«сжат» в 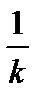 раз вдоль оси Оу (к оси Ох), если
раз вдоль оси Оу (к оси Ох), если 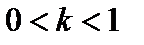 (рис. 4.16).
(рис. 4.16).
| y = f(x) |
| y = bf(x), 0 < b < 1 |
| y = bf(x), b > 1 |
| y |
| х |
Рис. 4.16
6. Для функции 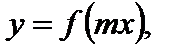 где
где 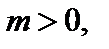 график
график 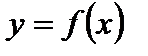 «растянут» вдоль оси Ох (от оси Оу) в
«растянут» вдоль оси Ох (от оси Оу) в 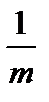 раз при
раз при 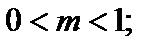 «сжат» вдоль Ох (коси Оу) в m раз, при
«сжат» вдоль Ох (коси Оу) в m раз, при 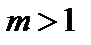 (рис. 4.17).
(рис. 4.17).
| y = f(ax), 0 <a <1 |
| y = f(ax), a > 1 |
| y = f(x) |
| y |
| x |
Рис. 4.17
7. Для функции 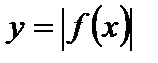 сохраняется та часть графика функции
сохраняется та часть графика функции 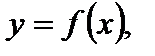 которая находится над осью Ох и на оси Ох, а та часть, которая находится под осью Ох, отображается симметрично оси Ох в верхнюю полуплоскость (рис. 4.18).
которая находится над осью Ох и на оси Ох, а та часть, которая находится под осью Ох, отображается симметрично оси Ох в верхнюю полуплоскость (рис. 4.18).
| y = |f(x)| |
| y = f(x) |
| y |
| x |
Рис. 4.18
8. Для функции 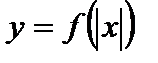 часть графика функции
часть графика функции 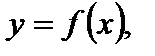 соответствующая отрицательному значению х, отбрасывается, а неотрицательному – сохраняется и дополняется симметричной ей относительно оси Оу частью (рис. 4.19).
соответствующая отрицательному значению х, отбрасывается, а неотрицательному – сохраняется и дополняется симметричной ей относительно оси Оу частью (рис. 4.19).
| y = f(x) |
| y |
| x |
| y = f(|x|) |
Рис. 4.19
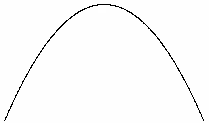
Пример 1. Построить график функции 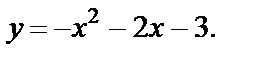
Решение. Преобразуем заданную функцию:
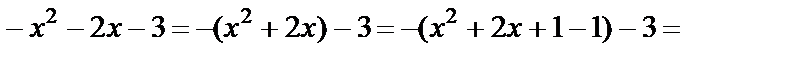
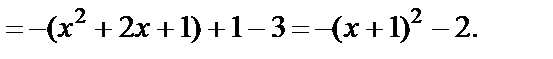
Получили 
Для построения графика полученной функции используем следующие преобразования:
1) строим график функции 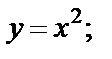
2) график функции 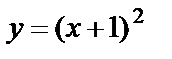 получаем из графика функции
получаем из графика функции 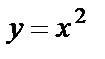 путем движения его на единицу влево по оси Ох;
путем движения его на единицу влево по оси Ох;
3) график функции 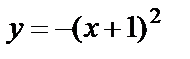 получаем из предыдущего симметричным отображением относительно оси Ох;
получаем из предыдущего симметричным отображением относительно оси Ох;
4) график заданной функции получаем из графика функции 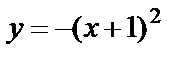 параллельным переносом на две единицы вниз по оси Оу (рис. 4.20).
параллельным переносом на две единицы вниз по оси Оу (рис. 4.20).
| –3 |
| х |
| –1 |
| –2 |
| у |
| 1) |
| 2) |
| 3) |
| 4) |
Рис. 4.20
Пример 2. Построить график функции 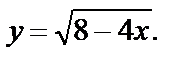
Решение. Вначале преобразуем формулу, задающую функцию:
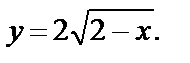
Шаги построения (рис. 4.21):
1) 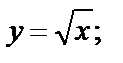
2) 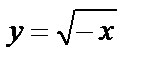 – отображение симметрично оси Оу в левую полуплоскость;
– отображение симметрично оси Оу в левую полуплоскость;
3) 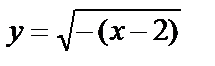 – смещение вдоль оси Ох вправо на две единицы;
– смещение вдоль оси Ох вправо на две единицы;
4) 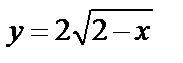 – увеличение коэффициента роста в два раза.
– увеличение коэффициента роста в два раза.

| –1 |
| –2 |
| 2) |
| 1) |
| x |
| у |
| 3) |
| 4) |
Рис. 4.21
Пример 3.Построить график функции 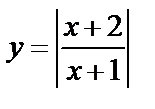 и найти наибольшее значение функции, если
и найти наибольшее значение функции, если 
Решение. 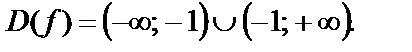
Преобразуем функцию
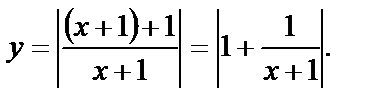
Данный график может быть получен из графика функции 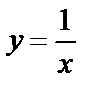 следующими преобразованиями (рис. 4.22):
следующими преобразованиями (рис. 4.22):
1) 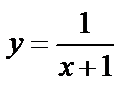 – смещение вдоль оси Ох на единицу влево;
– смещение вдоль оси Ох на единицу влево;
2) 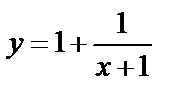 – смещение вдоль оси Оу вверх на единицу;
– смещение вдоль оси Оу вверх на единицу;
3) 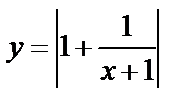 – отображение той части графика у3, которая расположена ниже оси Ох, в верхнюю полуплоскость (рис. 4.22). Заметим, что такие же преобразования необходимо применить к асимптотам функции
– отображение той части графика у3, которая расположена ниже оси Ох, в верхнюю полуплоскость (рис. 4.22). Заметим, что такие же преобразования необходимо применить к асимптотам функции 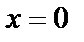 (вертикальной) и
(вертикальной) и 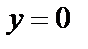 (горизонтальной).
(горизонтальной).
Анализ графика показывает, что наибольшее значение на 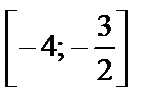 функция достигает в точке
функция достигает в точке 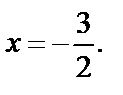 Вычисляем его:
Вычисляем его:
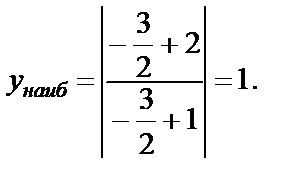
| –4 |
| –2 |
| х |
| у |
| 3) |
| 1) |
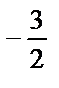
|
| –1 |
| 2) |
| f(–4) |
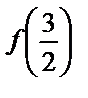
|
Рис. 4.22
Пример 4. Определить, при каком значении а уравнение имеет ровно 3 решения:
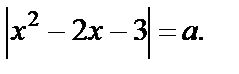
Решение. Решим задачу графически.
Построим графики функций 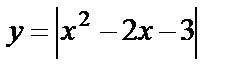 и
и 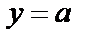 и исследуем, при каком значении а они имеют ровно 3 общие точки.
и исследуем, при каком значении а они имеют ровно 3 общие точки.
Строим график функции 
Поскольку 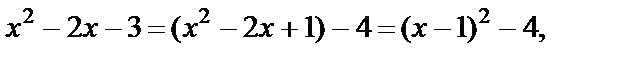 то
то
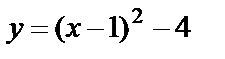 – это парабола, вершина которой смещена в точку
– это парабола, вершина которой смещена в точку 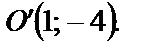
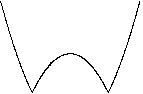
Для построения графика функции 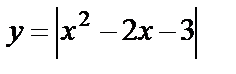 сохраняем ту часть графика параболы, которая находится над осью Ох и на оси Ох, а ту часть графика, которая находится под осью Ох, отображаем симметрично оси Ох в верхнюю полуплоскость.
сохраняем ту часть графика параболы, которая находится над осью Ох и на оси Ох, а ту часть графика, которая находится под осью Ох, отображаем симметрично оси Ох в верхнюю полуплоскость.
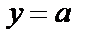 – прямая, параллельная оси Ох (рис. 4.23).
– прямая, параллельная оси Ох (рис. 4.23).
| –4 |
| у |
| –3 |
| а = 4 |
| –1 |
| х |
Рис. 4.23
По построению видно, что ровно 3 решения будет тогда и только тогда, когда 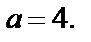
Дата добавления: 2015-09-29; просмотров: 972;
