Действия над комплексными числами в алгебраической
Форме
Пусть 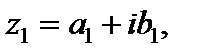
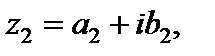 тогда:
тогда:
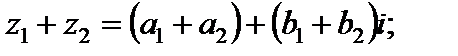 (1.13)
(1.13)
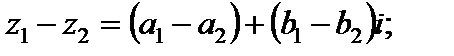 (1.14)
(1.14)
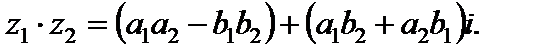 (1.15)
(1.15)
Формулы (1.13)–(1.15) показывают, что операции сложения, вычитания и умножения выполняются аналогично таким же действиям над многочленами (с учетом 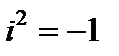 при умножении).
при умножении).
Для нахождения частного комплексных чисел 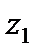 и
и 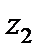 сначала числитель и знаменатель дроби
сначала числитель и знаменатель дроби 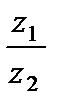 умножают на сопряженное знаменателю число
умножают на сопряженное знаменателю число  а затем производят остальные действия:
а затем производят остальные действия:
 (1.16)
(1.16)
Свойства комплексно-сопряженных чисел:
1) 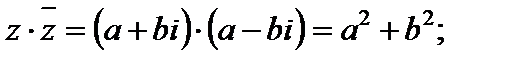 2)
2) 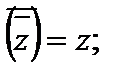
3) 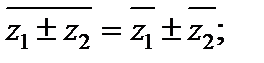 4)
4) 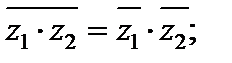
5) 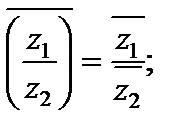 6)
6) 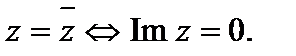
Пример 1. Найти 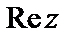 и
и 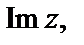 если
если
1) 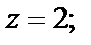 2)
2) 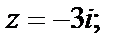 3)
3) 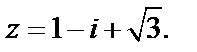
Решение. 1) Так как  то
то 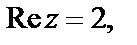
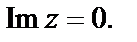
2) Поскольку 
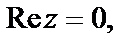

3) Запишем число в стандартном виде: 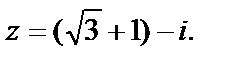 Поэтому
Поэтому 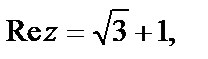
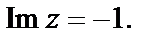
Пример 2.Даны комплексные числа 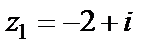 и
и 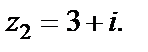 Найти:
Найти:
1)  2)
2) 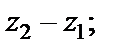 3)
3) 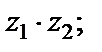 4)
4) 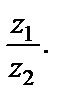
Решение. 1) 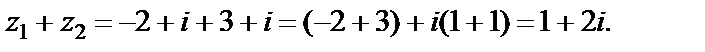
2) 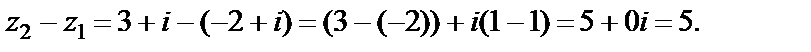
3) Перемножим числа 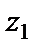 и
и 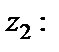
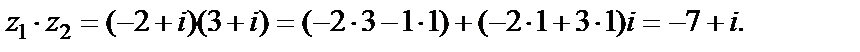
4) Для нахождения частного 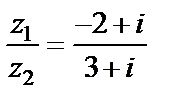 умножим числитель и знаменатель дроби на
умножим числитель и знаменатель дроби на  (т. е. на число, сопряженное знаменателю). Тогда получим
(т. е. на число, сопряженное знаменателю). Тогда получим
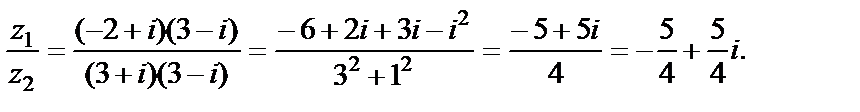
Пример 3. Найти число, сопряженное числу 
Решение. Умножив числитель и знаменатель дроби на  получим
получим
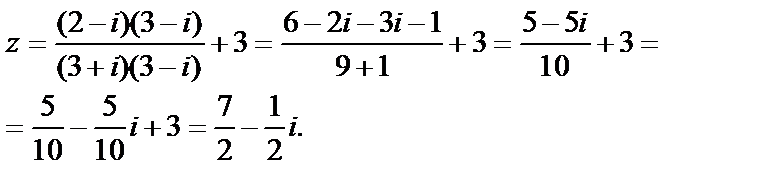
Тогда 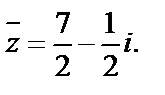
Пример 4. Вычислить  для n Î N.
для n Î N.
Решение.При вычислении используем, что, согласно определению, 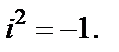 Тогда
Тогда
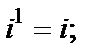

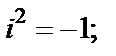
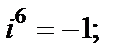


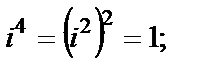
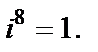
Очевидно, что значения степени повторяются циклически:

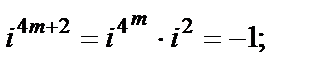
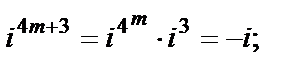
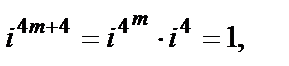
где 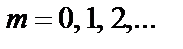 .
.
Пример 5. Найти множество точек, для которых 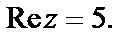
Решение. Поскольку 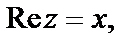 точки искомого множества лежат на прямой
точки искомого множества лежат на прямой 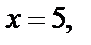 параллельной мнимой оси (рис. 1.11).
параллельной мнимой оси (рис. 1.11).

| х |
| у |
| Re z = 5 |
Рис. 1.11
Пример 6. Показать на координатной плоскости множество всех точек, которые находятся на расстоянии, равном 3, от точки 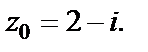
Решение. Пусть 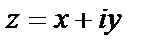 – одна из искомых точек. На плоскости ей соответствует точка с координатами
– одна из искомых точек. На плоскости ей соответствует точка с координатами  Точке
Точке 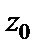 соответствует точка плоскости с координатами
соответствует точка плоскости с координатами 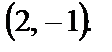 В качестве решения задачи подходят все точки, для которых
В качестве решения задачи подходят все точки, для которых
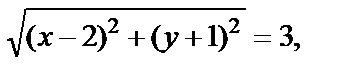 т. е.
т. е. 
Полученному уравнению соответствует множество точек окружности с центром в точке  и радиусом 3 (рис. 1.12).
и радиусом 3 (рис. 1.12).
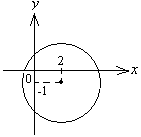
Рис. 1.12
Дата добавления: 2015-09-29; просмотров: 949;
