Гідравліка. Основні закони і поняття 5 страница
D - діаметру поршня циліндра, см;
Dш - діаметру штока циліндра, см;
d - внутрішнього діаметру трубопроводу, см;
Δ - товщина стінки циліндра, см;
δ - товщина стінки труби, см|труба-конденсатора|.
Для визначення вище перелічених геометричних параметрів заздалегідь обчислюють площу поршня F, см2, площу трубопроводу f, см2 і коефіцієнт підвідного штока Кш по виразах:
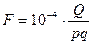 , (3.2)
, (3.2)
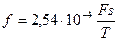 , (3.3)
, (3.3)
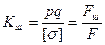 , (3.4)
, (3.4)
де Q – повне|цілковите| навантаження на шток циліндра, MH|;
р - тиск повітря в пневмоциліндрі, МН/м2;
q - параметр завантаження|загрузки| циліндра;
s - хід поршня, см;
Т - час робочого циклу, с|із|;
[σ]- напруга, що допускається, для матеріалу циліндра, МН/м2;
Fш - площа перетину штока, см2.
Остаточний розрахунок геометричних параметрів пневмопривода| ведуть за формулами:
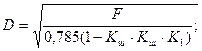 (3.5)
(3.5)
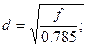 (3.6)
(3.6)
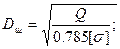 (3.7)
(3.7)
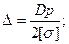 (3.8)
(3.8)
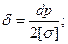 (3.9)
(3.9)
K1 - коефіцієнт, що враховує вид робочої порожнини циліндра.
При прямому ході штока циліндра (коли стисле повітря подається в поршневу порожнину) К1 = 1, а при зворотному ході – К1 =0.
Час робочого циклу складе, с:
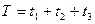 , (3.10)
, (3.10)
де t1 - час наростання тиску в циліндрі до початку руху поршня (час вистою), с;
t2 - час руху поршня, с;
t3 - час наростання тиску в циліндрі до магістрального після зупинки поршня (час наслідку), с.
Час вистою| визначається по формулі:
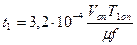 , (3.11)
, (3.11)
де Von - об'єм, що спорожнюється при простої поршня порожнини циліндра, см3;
Т1оп - параметр часу вистою;
μ - витратний коефіцієнт трубопроводу.
Величини µ і Т1оп можуть бути представлені у вигляді:
μ = 0,64-0,314lgε при ε ≤ 35 (3.12)
μ = 0,323-0,097lgε при ε > 35 (3.13)
Т1оп = 0,175q – 0,0075 при q ≤ 0.5 (3.14)
Т1оп = 0,3q-0,07 при q> 0.5 (3.15)
де ε – коефіцієнт опору системи.
Величина Von визначається по формулі:
Von = Fs (1 – Kш K1 ) + 100fl , (3.16)
де l- довжина трубопроводу, м.
На підставі залежностей (3.11, 3.14-3.16) отримаємо|одержуватимемо|:
при q > 0.5
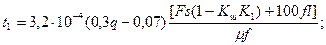 (3.17)
(3.17)
при q ≤ 0.5
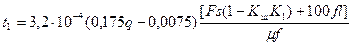 . (3.18)
. (3.18)
Час руху поршня t2 визначають залежно від конструктивного параметра N:
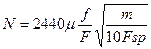 , (3.19)
, (3.19)
де m - маса рухомих|жвавих| частин, кг|часток|.
Розглядають|розглядують| два випадки: при N < 1 і N ≥ 1.
При N < 1
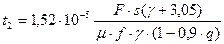 ; (3.20)
; (3.20)
при N ≥ 1
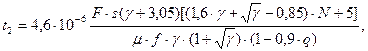 (3.21)
(3.21)
де γ - співвідношення площ|майданів| перетину напірної і вихідної магістралі| (розрахункові залежності справедливі при γ = 0.25...10).
Час післядії t3 визначають як найбільше з двох величин часу наростання тиску до магістрального в порожнині наповнення t3н і часу падіння тиску до атмосферного в порожнині спорожнювання t3оп. Для визначення цих величин можна скористатися формулами:
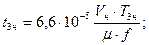 (3.22)
(3.22)
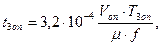 (3.23)
(3.23)
де Vн - об'єм порожнини наповнення, см3;
Von - об'єм порожнини спорожнення, см3;
Т3н - параметр часу вистою;
Т3оп - параметр часу падіння тиску.
Об'єми порожнин циліндра складають:
Vн = F · s · (1 + Kш · K1 – Kш ) + 100 f · l; (3.24)
Vоп = 100 · f · l . (3.25)
Параметри часу розглядаються для 2-х випадків залежно від величини параметра завантаження q:
при q ≤ 0.5
Т3н = 0,251 - 0,0625 · q; (3.26)
Т3оп = 0,15 · q + 0,005; (3.27)
при q>0.5
Т3н = 0,345 - 0,25 · q; (3.28)
Т3оп = 0,35 · q - 0,095; (3.29)
При підстановці залежностей (3.24-3.29) у вирази (3.22, 3,23) отримаємо|одержуватимемо|:
при q > 0.5
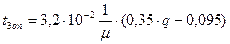 ;(3.30)
;(3.30)
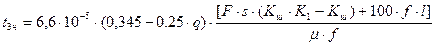 (3.31)
(3.31)
при q ≤ 0.5
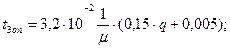 (3.32)
(3.32)
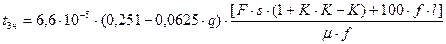 . (3.33)
. (3.33)
В процесі обчислення|підрахунку| виконують порівняння дійсного робочого циклу Т із|із| заданим t і при необхідності його коригують|.
Порівняння ведеться по формулах:
при T > t
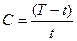 , (3.34)
, (3.34)
при Т < t
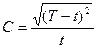 . (3.35)
. (3.35)
Коригування Т здійснюється у випадку, якщо|у разі , якщо| величина С|із| перевищує допустиме значення. При Т > t приймають С|із| = 0,05 і коректують Т спочатку шляхом зменшення величини q, а потім збільшенням величини f.
При T<t| приймають С|із| = 0,1 і коригують Т| спочатку шляхом|колією| збільшення q, а потім зменшенням f. 1
При розрахунку на ЕОМ крок зміни q для коректування Т в обох випадках приймають Δq = 0,01. Зміну величини q обмежують межами 0,4 ≤ q ≤ 0,7, а її первинне значення набувають рівним 0,5.
4 ЛАБОРАТОРНИЙ ПРАКТИКУМ
4.1 Вивчення режимів руху рідини
Мета роботи: Вивчити режими руху рідини на установці Рейнольдса.
4.1.1 Загальні відомості
В даний момент часу в кожній точці в межах потоку, що рухається, перебуває частка рідини, що має деяку швидкість u. Ця швидкість називається миттєвою місцевою швидкістю. Сукупність миттєвих місцевих швидкостей представляє векторне поле, що називається полем швидкостей.
За характером зміни поля швидкостей у часі рух рідини ділиться на неусталений й усталений.
Неусталений (нестаціонарний)рух такий, при якому в точках області, де рухається рідина, місцеві швидкості змінюються із часом. При неусталеному русі всі елементи руху (швидкість u, прискорення j, тиск p, глибина h) є функцією й координат (x, y, z) і часу t.
Якщо в будь-якій точці потоку рідини швидкість, тиск і прискорення залишаються постійними, тобто не змінюються в часі ні по величині, ні по напрямку, то такий рух розглядається як сталий (стаціонарний).
Сталий рух може бути рівномірним і нерівномірним.
Рівномірним називається такий усталений рух, при якому живі перетини потоку й середня швидкість v у них однакові по його довжині. Нерівномірним називається такий усталений рух рідини, при якому живі перетини й середні швидкості потоку v змінюються по його довжині.
Якщо потік з усіх боків обмежений твердими стінками, то він називається напірним. Якщо тільки частина потоку обмежена твердими стінками, а на іншій частині рідина граничить із газом, зокрема, з атмосферою (потік має вільну поверхню), то такий рух називається безнапірним.
Живим перетином потоку w називають поперечний переріз потоку, перпендикулярний його напрямку.
Об'ємною витратою потоку Q називають об'єм рідини V, що проходить в одиницю часу t через живий перетин потоку, (м3/с):
Q = 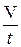 (4.1)
(4.1)
Змочений периметр c (хі) – частина периметра живого перетину, на якому рідина стикається із твердими стінками.
Гідравлічним радіусомR називають відношення площі живого перетину потоку w до змоченого периметра c
R= 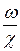 (4.2)
(4.2)
Відношення чотирьох площин живого перетину потоку до змоченого периметра 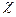 називається діаметром еквівалентнимdекв
називається діаметром еквівалентнимdекв
dекв = 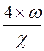 = 4´R (4.3)
= 4´R (4.3)
Середньою швидкістю v потоку в даному перетині називають відношення об'ємної витрати потоку Q до площі його живого перетину w
v = 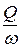 (4.4)
(4.4)
Втрати енергії при русі рідини залежать від режиму руху.
Розрізняють два режими руху рідини: ламінарний і турбулентний (табл.1.1).
Рейнольдс установив, що перехід від ламінарного плину до турбулентного й навпаки визначається середньою швидкістю плину v, характерним поперечним розміром потоку L, фізичними властивостями рідини: густиною r і в'язкістю (динамічний коефіцієнт в'язкості h або кінематичний коефіцієнт в'язкості n). У загальному випадку режим руху рідини визначається безрозмірним комплексом, складеним із зазначених величин і називаним числом(критерієм) Рейнольдса
Re = 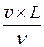 =
= 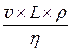 (4.5)
(4.5)
Число Рейнольдса характеризує відношення сил інерції до сил тертя (в'язкості). Перехід від одного режиму руху в інший визначається перевагою сили інерції або сили тертя.
У якості характерного геометричного розміру живого перетину потоку L найчастіше приймають діаметр труби d (для круглих напірних труб), для некруглих і безнапірних труб гідравлічний радіус R або діаметр еквівалентний dекв. Тоді, відповідно
Red = 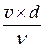 ,
, 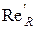 =
= 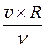 , Red екв =
, Red екв = 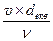 .
.
Швидкість потоку, при якій відбувається зміна режиму руху рідини, називається критичною. Рейнольдс виявив існування двох критичних швидкостей: верхньої критичної швидкості – при переході ламінарного режиму руху в турбулентний, і нижньої критичної швидкості – при переході турбулентного режиму руху в ламінарний. Відповідно розрізняють верхнє й нижнє критичні числа Рейнольдса.
Для круглих напірних труб при усталеному рівномірному русі рідини 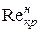 =2000…2320, а
=2000…2320, а 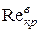 = 4000…100000.
= 4000…100000.
Значення 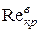 (перехід ламінарного плину в турбулентний) залежить від зовнішніх умов досліду: сталості температури, рівня вібрації установки, умов входу в трубу, шорсткості поверхні стінок труби, стану рідини в резервуарі, що живить трубу й т.п. Значення
(перехід ламінарного плину в турбулентний) залежить від зовнішніх умов досліду: сталості температури, рівня вібрації установки, умов входу в трубу, шорсткості поверхні стінок труби, стану рідини в резервуарі, що живить трубу й т.п. Значення 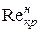 (перехід турбулентного руху в ламінарний) від цих величин практично не залежить.
(перехід турбулентного руху в ламінарний) від цих величин практично не залежить.
У практичних умовах, де завжди є джерела випадкових збурювань, варто вважатися тільки з нижньою границею.
Таким чином, як критичне число Рейнольдса прийняте 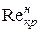 для циліндричних напірних труб
для циліндричних напірних труб
Reкр = 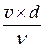 = 2000…2320.
= 2000…2320.
Для будь-якого потоку по відомим v, L й n можна обчислити число Рейнольдса й зрівняти його із критичним значенням Reкр. Якщо Re < Reкр, то
v < vкр і режим руху рідини ламінарний; якщо Re > Reкр, те v > vкр і режим руху турбулентний.
4.1.2 Опис лабораторної установки
Установка, що зображена на рис. 4.1, призначена для візуального спостереження режиму плину рідини.
У циліндричну скляну трубку через плавний коноїдальний вхід рідина подається з резервуара 1, де вона заспокоюється за допомогою системи решіток. Резервуар (бак) 1 має досить великий розмір. Висота рівня рідини в баці підтримується постійною. Наприкінці скляної труби 2 установлений кран 3 для регулювання витрати потоку. Вимір витрати виконується за допомогою мірного бака 4 і секундоміра.
У вхідну ділянку труби через тонку трубочку 5 з посудини 6 подається підфарбована рідина із щільністю й швидкістю витікання, близькими до цих же характеристик потоку рідини в трубі. Витрата фарби регулюється краном 7. Підфарбований струмок рідини дозволяє зробити видимою структуру потоку в трубі.
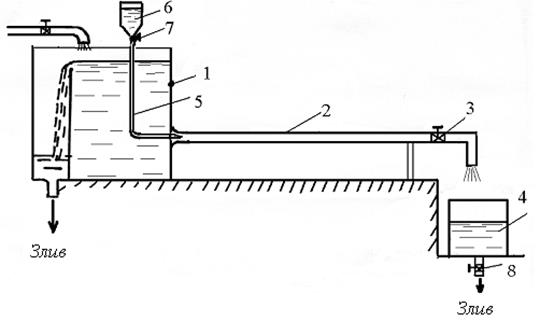
1 - резервуар (бак); 2 - скляна трубка; 3 - кран для регулювання витрати потоку; 4 - мірний бак; 5 - трубка для подачі підфарбованої рідини; 6 - посудина з розчином підфарбованої рідини; 7 - кран для регулювання подачі підфарбованої рідини; 8 - кран на мірному бачку
Рисунок 4.1 - Установка Рейнольдса для вивчення режимів руху рідини
При невеликих значеннях швидкості v підфарбований струмок має вигляд нитки із чітко обкресленими границями. Рідина рухається окремими шарами, що не перемішуються. При більших швидкостях підфарбований струмок починає викривлятися й стає хвилеподібним. Це відбувається в результаті змін у часі (пульсації) векторів місцевих швидкостей у потоці.
Наявність поперечних пульсацій є відмітною рисою турбулентного плину. Тому поява поперечних коливань підфарбованого струмка рідини служить вказівкою на перехід ламінарного режиму в турбулентний.
При подальшому збільшенні швидкості потоку струмок розпадається на окремі добре видні вихорі, відбувається перемішування пофарбованого струмка з усією масою поточної рідини. На невеликій відстані від входу (10-20 діаметрів труби) потік виявляється рівномірно пофарбованим.
4.1.3 Порядок виконання лабораторної роботи
1. При закритому крані (3) заповнюють напірний бак водою так, щоб безупинно працював злив.
2. Злегка відкривши вентиль (3), створюють невелику витрату води по трубі (кран (8) на мірному бачку відкритий).
3. Відкриттям крана (7) домагаються одержання тонкого струмка фарби, що не розривається. За візуальними спостереженнями встановлюють ламінарний режим.
4. При даному режимі руху рідини закривають кран (8) на мірному баці. Замірять висоту підйому рідини в мірному бачку h за відповідний час t.
5. За допомогою крана (8) установлюють за візуальними спостереженнями турбулентний режим і повторюють виміри (3...4 рази).
6. Термометром замірять температуру води 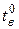 й по табл.4.3 визначають значення коефіцієнта кінематичної в'язкості води n.
й по табл.4.3 визначають значення коефіцієнта кінематичної в'язкості води n.
Результати вимірів заносять у таблицю 4.1.
4.1.4 Обробка результатів експерименту
1. Визначають об'єм води V, що витекла в мірний бачок за час t при і-му вимірі, м3:
V = hi´wб,
де h – висота підйому води в мірному бачку при і-м вимірі, м;
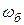 - площа перетину мірного бачка, м2.
- площа перетину мірного бачка, м2.
Таблиця 4.1 - Результати вимірів і довідкові величини
| Номер досліду | Режим руху рідини за візуальними спостереженнями | Час наповнення мірного бачка t, с | Висота підйому води в мірному бачку hi, м | Площа мірного бачка wб, м2 | Діаметр труби d, м | Температура води, t0в 0С | Кінематичний коефіцієнт в'язкості води n, м2/с |
2. Визначають об'ємну витрату Q при і-му вимірі, м3/с:
Q = 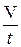 ,
,
де t – час наповнення мірного бака, c.
3. Визначають середню швидкість руху води по трубі v при і-му вимірі з рівняння сталості об'ємної витрати, м/с:
v = 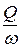 =
= 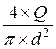 ,
,
де w - площа поперечного переріза труби, м2.
4. Розраховують число Рейнольдса:
Re = 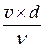
5. Розраховане значення критерію Рейнольдса порівнюють із критичним й роблять висновок про режим плину рідини (з розрахунку).
6. Поставити графік залежності Re = f(v) і визначити критичну швидкість переходу з ламінарного режиму руху в турбулентний.
7. Результати розрахунку зводять у табл. 4.2.
Таблиця 4.2 - Результати розрахунків
| Номер досліду | Режим руху рідини (за візуальними спостереженнями) | Об'єм води в мірному баці V, м3 | Об'ємна витрата Q, м3/с | Середня швидкість руху води v, м/с | Значення критерію Рейнольдса, Re | Режим руху рідини (з розрахунку) |
Таблиця 4.3 – Кінематичний коефіцієнт в'язкості n води, 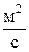
| t0, 0C | n´108 | t0, 0C | n´108 | t0, 0C | n´108 | t0, 0C | n´108 |
4.1.5 Зміст звіту
Короткі теоретичні відомості. Схема лабораторної установки та її опис. Таблиці вимірів і розрахунків. Графік залежності Re = f(v). Висновок.
4.1.6 Контрольні питання
1. Режими руху та їхні особливості.
2. Критерій Рейнольдса та його фізичний зміст.
3. Поняття характерного розміру трубопроводу.
4. Поняття усталеного й неусталеного руху.
5. Поняття рівномірного й нерівномірного руху.
4.2 Визначення коефіцієнта гідравлічного тертя
Мета роботи: Вивчити залежність коефіцієнта гідравлічного тертя від числа Рейнольдса.
4.2.1 Загальні теоретичні відомості
При русі реальної рідини частина енергії потоку губиться на подолання сил тертя. Втрати питомої енергії (напору) на ділянці між двома довільно обраними перетинами 1-1 й 2-2 (рис. 4.2) визначають із рівняння Бернуллі, м:
Dhтр = НР 1 - НР 2 = 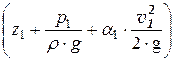 -
- 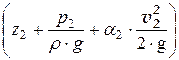
Для горизонтальної труби постійного діаметра при 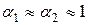 одержують:
одержують:
Dhтр = 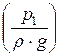 -
- 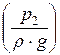 .
.
Втрати напору по довжині (лінійні втрати) Dhтр визначаються формулою Дарсі-Вейсбаха, м:
Dhтр = l× 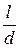 ×
× 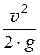 ,(4.6)
,(4.6)
де 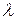 - коефіцієнт гідравлічного тертя (коефіцієнт Дарсі);
- коефіцієнт гідравлічного тертя (коефіцієнт Дарсі);
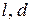 - довжина й діаметр трубопроводу відповідно, м;
- довжина й діаметр трубопроводу відповідно, м;
v – середня швидкість плину рідини в перетині потоку, м/с.
Коефіцієнт гідравлічного тертя 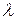 залежить від в'язкості
залежить від в'язкості 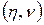 й густини рідини
й густини рідини 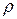 , діаметра трубопроводу d, шорсткості внутрішніх стінок трубопроводу kе й середньої швидкості руху рідини v. У загальному випадку коефіцієнт залежить від двох безрозмірних параметрів – числа Рейнольдса Re і відносної шорсткості
, діаметра трубопроводу d, шорсткості внутрішніх стінок трубопроводу kе й середньої швидкості руху рідини v. У загальному випадку коефіцієнт залежить від двох безрозмірних параметрів – числа Рейнольдса Re і відносної шорсткості 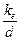 :
:
l = f 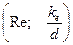 ,
,
де 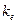 - абсолютна еквівалентна шорсткість стінок труби, м (табл. 4.4).
- абсолютна еквівалентна шорсткість стінок труби, м (табл. 4.4).
Під абсолютною еквівалентною шорсткістю розуміють таку уявлювану (умовну) рівномірну шорсткість, при якій втрати напору дорівнюють втратам у реальному трубопроводі за тих самих умов плину.
При ламінарному режимі плину рідини (Re<Reкр) коефіцієнт гідравлічного тертя залежить тільки від числа Рейнольдса й визначається по формулі:
l = 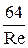 (4.7)
(4.7)
По найпоширенішій гіпотезі Прандтля турбулентний потік (Re>Reкр) ділять на турбулентне ядро й в’язкий підшар. Товщина в’язкого підшару 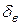 залежить від числа Рейнольдса.
залежить від числа Рейнольдса.
При відносно невеликих швидкостях (невеликих числах Re) в’язкий підшар повністю закриває всі виступи шорсткості стінки. В результаті вплив шорсткості на коефіцієнт гідравлічного тертя 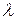 й, відповідно, на втрати напору по довжині буде зневажливо малий.
й, відповідно, на втрати напору по довжині буде зневажливо малий.
Ця зона турбулентного руху рідини називається зоною гідравлічно гладких труб. Критерій зони турбулентності 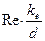 менше 10. Коефіцієнт гідравлічного опору визначається по формулі Блазіуса:
менше 10. Коефіцієнт гідравлічного опору визначається по формулі Блазіуса:
l = 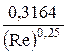 (4.8)
(4.8)
Таблиця 4.4 – Значення абсолютної еквівалентної шорсткості kе
| Матеріал і вид труби | Стан труби | kе, мм |
| Тягнені труби з кольорових металів | Нові технічно гладкі | 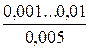 * *
|
| Безшовні сталеві труби | Нові й чисті | 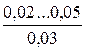
|
| Після декількох років експлуатації | 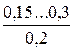
| |
| Сталеві труби зварені | Нові й чисті | 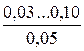
|
| З незначною корозією після очищення | 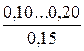
| |
| Помірно заіржавлені | 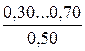
| |
| Старі, заіржавлені | 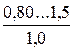
| |
| Сильно заіржавлені або з великими відкладеннями | 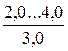
| |
| Клепані сталеві труби | Клепані уздовж і поперек по одному ряді заклепок: гарний стан поверхні | 0,30...0,40 |
| З подвійною поздовжньою клепкою й простою поперечною клепкою; некородовані | 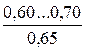
| |
| Із простою поперечною й подвійною поздовжньою клепкою; зсередини просмолені або покриті лаком | 1,20...1,30 | |
| Оцинковані сталеві труби | Нові й чисті | 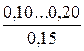
|
| Після декількох років експлуатації | 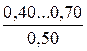
| |
| Чавунні труби | Нові | 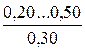
|
| Що були у вживанні | 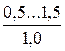
| |
| Дуже старі | до 3,0 |
* - у чисельнику наведений діапазон значень kе;під рисою наведені середні значення kе.
Дата добавления: 2015-09-07; просмотров: 1095;
