Лекция 5. « Строение и виды теорем»

« Строение и виды теорем»

1.

Определение. Импликацией предикатов А(х) и В(х) называют предикат А(х) Þ В (х), определенный на множестве и обращающийся в ложное высказывание при тех и только тех х, при которых А(х) обращается в истинное высказывание, а В (х) – в ложное.

Определение. Если импликация А(х) Þ В (х) истинна для всех значений хÎХ, то говорят что предикат В (х) следует из предиката А(х).

Если Т 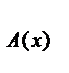- множество истинности высказывательной формы А(х), а Т_В(х)- множество истинности высказывательной формы В(х), то Т_{А(х)ÞВ(х)} = Т_Ā(х) Ú Т_В(х).

Пример: На множестве Х={1,2,3,4,5,6,7,8.} заданы высказывательные формы А(х)- х < 6, и В(х)- х – четное число. Найти Т_{А(х)ÞВ(х)}

Решение: найдем Т_А(х) , Т_Ā(х) и Т_В(х).

Т_А(х) ={1,2,3,4,5.}

Т_Ā(х) ={6,7,8.}

Т_В(х)= {2,4,6,8.}

А(х) Þ В(х) – если х число четное , то оно меньше шести.

Т_{А(х)ÞВ(х)} ={2,4,6,7,8.}

Определение.Эквиваленцией предикатовР(х) и Q(х) называют предикат Р(х) Û Q (х), определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех х, при которых Р(х) и Q(х) обращаются оба в истинные высказывания или оба в ложные.