Моделирование дискретных сигналов в MATLAB

Генерировать сигналы в MATLAB можно тремя способами:

– в диалоговом режиме, с помощью последовательности команд в командном окне;

– в автоматическом режиме, путем создания и запуска на выполнение m-скрипта;

– в автоматическом режиме, путем создания и вызова m-функции.

Генерирование сигналов в диалоговом режиме. Этот способ наиболее трудоемок, поскольку требует каждую команду набирать с клавиатуры в командном окне. Чтобы повысить производительность труда, можно всю последовательность команд предварительно набрать в любом текстовом редакторе (обычно это Notebook или Word), а затем, скопировав текст в буферную память (Clipboard), вставить его в командное окно. Недостаток этого способа в том, что необходимо одновременно держать активными две программы – MATLAB и текстовый редактор. Достоинство данного способа проявляется тогда, когда работу в MATLAB производят, следуя некоей инструкции, в которой теоретические сведения чередуются с практическими заданиями в виде фрагментов текстов m-скриптов.

Например, так выглядит в текстовом редакторе последовательность команд генерирования N отсчетов тонального сигнала амплитудой A, частотой f0, начальной фазой Fi0, с частотой дискретизации Fs:

% гармонический сигнал

A=1; f0=100; Fi0=pi/2; Fs=1000; N=20; % параметры сигнала

t=(0:N-1)/Fs; % моменты времени

s=A*sin(2*pi*f0*t+Fi0); % вычисление отсчетов

%сигнала

plot(t,s) % вывод графика

title('Гармонический сигнал') % заголовок

xlabel('ВремЯ, с'); ylabel('Уровень'); % надписи вдоль осей

grid on % координатнаЯ сетка

Полученный график отображается в специальном окне с надписью Figure #1 (если это первый строящийся график). График удобно сохранять путем экспорта в экономном формате *.jpg (рис.2).

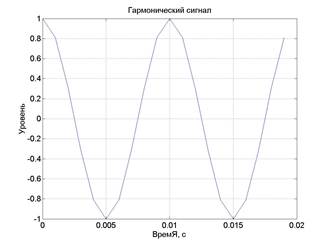
Рис.2. График сигнала тональной частоты

Примечание: при использовании символов кириллицы в тексте команд (комментарии, заголовки и т.п.) следует учитывать особенности «отношения» каждой конкретной версии MATLAB к кириллице. Так, в MATLAB версии 6.1 нельзя употреблять строчную букву «я» – вместо нее следует писать прописную букву «Я». Именно по этой причине в тексте на рис. 2 вместо «Время» получилось «ВремЯ». Впрочем, эту надпись можно отредактировать (кнопка со стрелкой Edit Plot в графическом окне) перед тем, как сохранять рисунок на диске.

Генерирование сигналов путем создания m-скрипта.Данный способ отличается тем, что все команды набираются в специальном окне редактора m-файлов (рис.3).

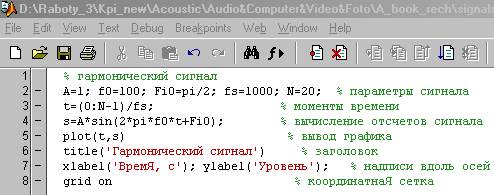
Рис.3. Набор команд в окне редактора m-файлов

Данный способ удобен тем, что вместо сторонних программных продуктов используется собственный инструментарий MATLAB, специализированный для написания и отладки m-скриптов.

Генерирование сигналов путем создания m-функции.Данный способ отличается тем, что входные данные записывают как аргумент некоей функции 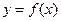, а выходные – как значение этой функции. Удобство в том, что символьные обозначения данных могут отличаться от обозначений, используемых в теле функции. Более того, числовые значения входных данных можно просто задавать в наименовании вызываемой функции. Последнее обстоятельство продемонстрируем на примере.

Создадим подпрограмму – m-скрипт ton.m вида:

% скрипт ton

s=A*sin(2*pi*f0*t+Fi0); % вычисление отсчетов сигнала

Команду выполнения этого скрипта нужно «окружить» командами подготовки входных данных и вывода выходных данных:

A=1; f0=100; Fi0=pi/2; Fs=1000; N=20; % параметры сигнала

t=(0:N-1)/Fs; % моменты времени

ton; % вычисление отсчетов

%сигнала

plot(t,s) % вывод графика

title('Гармонический сигнал') % заголовок

xlabel('ВремЯ, с'); ylabel('Уровень'); % надписи вдоль осей

grid on % координатнаЯ сетка

Очевидно, обозначения входных и выходных данных вызывающей программы должны совпадать с обозначениями соответствующих данных вызываемой подпрограммы.

Теперь поступим по-иному – напишем и сохраним m-функцию под именем ton_sig.m:

%-------функциЯ ton_sig.m -----------

% [s,t]=ton_sig(B,f1,Fi1,Fs,N1)

%---------------------------------------

% генерирование гармонического сигнала

% y = B * sin(2*pi*f1*x + Fi1),

% B - амплитуда;

% N1 - количество отсчетов сигнала;

% f1 - частота;

% Fs - частота дискретизации;

% Fi1 - начальнаЯ фаза сигнала

%---------------------------------------

function [y,x] = ton_sig( B, f1, Fi1, Fs, N1 )

%---------------------------------------

x = (0:N1-1)/Fs; % моменты времени

y = B * sin( 2*pi*f1*x + Fi1 );

%-------- конец функции ton_sig.m ----------

Теперь m-скрипт генерирования того же отрезка косинусоиды будет выглядеть так:

% гармонический сигнал

[s,t]=ton_sig(1,100,pi/2,1000,20) % вычисление отсчетов сигнала

plot(t,s) % вывод графика

title('Гармонический сигнал') % заголовок

xlabel('ВремЯ, с'); ylabel('Уровень'); % надписи вдоль осей

grid on % координатнаЯ сетка

Как видим, теперь числовые значения входных данных задаются как аргументы m-функции ton_sig.m. Выходные данные функции используются для построения графика.

Очевидно, применение m-функций предпочтительно в том случае, когда алгоритм формирования значений функции достаточно сложный, содержится много команд и обращений к разнообразным библиотечным функциям с непростым синтаксисом.

Очевиден и недостаток m-функций – необходимо помнить их синтаксис. Впрочем, получить нужную информацию можно, если в командном окне задать команду help:

>> help ton_sig

В результате на мониторе отобразится комментарий, с которого начинается m-функция. Для приведенного выше примера текст помощи имеет следующий вид:

%-------функциЯ ton_sig.m -----------

% [s,t]=ton_sig(B,f1,Fi1,Fs,N1)

%---------------------------------------

% генерирование гармонического сигнала

% y = B * sin(2*pi*f1*x + Fi1),

% B - амплитуда;

% N1 - количество отсчетов сигнала;

% f1 - частота;

% Fs - частота дискретизации;

% Fi1 - начальнаЯ фаза сигнала

%---------------------------------------

Таким образом, очевиден вывод: очень важно при программировании m-функций снабжать их качественным и подробным комментарием.