Синтез одноразрядного сумматора
Сумматор — это электронная логическая схема, выполняющая суммирование двоичных чисел.
Сумматор является центральным узлом арифметико-логического устройства компьютера.
Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров.
Условное обозначение одноразрядного сумматора:
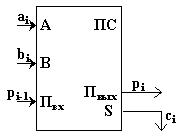
При сложении чисел A и B в одном i-ом разряде приходится иметь дело с тремя цифрами:
· цифра ai первого слагаемого;
· цифра bi второго слагаемого;
· перенос pi–1 из младшего разряда.
В результате сложения получаются две цифры:
· цифра ci для суммы;
· перенос pi из данного разряда в старший.
Таким образом, одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами, работа которого может быть описана следующей таблицей истинности:
| Входы | Выходы | |||
| Первое слагаемое | Второе слагаемое | Перенос | Сумма | Перенос |
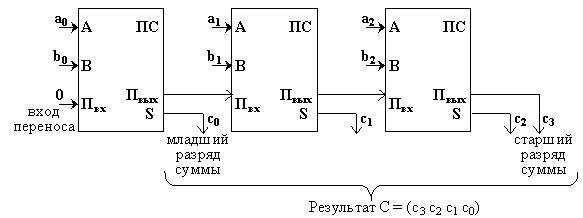
Если требуется складывать двоичные слова длиной два и более бит, то можно использовать последовательное соединение таких сумматоров, причём для двух соседних сумматоров выход переноса одного сумматора является входом для другого.
Например, схема вычисления суммы C = (с3 c2 c1 c0) двух двоичных трехразрядных чисел A = (a2 a1 a0) и B = (b2 b1 b0) может иметь вид:
Постановка задачи:
Синтезировать комбинационную схему одноразрядного двоичного сумматора, имеющего два входа («а» и «b») и два выхода («S» - значение суммы и «Р» - перенос в следующий разряд.
Порядок выполнения работы:
1. Сформировать таблицу истинности.
2. Получить совершенные дизъюнктивные формы логических функций (СДНФ), реализуемых одноразрядным двоичным сумматором.
3. Используя диаграммы Вейча, минимизировать логические выражения (СДНФ).
4. Используя базовый набор элементов И, ИЛИ, НЕ составить структурную схему одноразрядного двоичного сумматора комбинационного типа.
1. Одноразрядный двоичный сумматор реализует следующую таблицу сложения:
| a + b | a | ||
| b | |||
При сложении двух единиц образуется разряд суммы S = 0 и перенос P = 1 в следующий разряд.
Следовательно, одноразрядный комбинационный сумматор реализует две логических функции, таблицы истинности которых имеют вид:
| а | b | f1(a, b) = S | f2(a,b) = P |
Здесь f1(a, b) = S - значение цифры суммы в данном разряде;
f2(a, b) = P - цифра переноса в следующий (старший) разряд.
2. СДНФ для этих функций имеют вид:
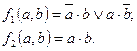
3. Диаграммы Вейча для этих функций имеют вид:
| f1(a, b) = S | f2(a, b) = P | ||||
| b | 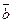
| b | ||
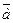
| 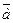
| ||||
| а | а |
В этих диаграммах конституенты единицы не склеиваются. Следовательно, полученные СДНФ являются минимальными.
4. Логическая схема сумматора, реализующего полученные функции, представлена на рис. 7.
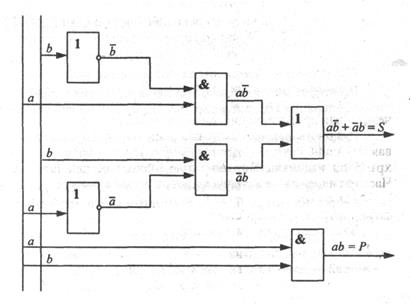
Рис. 7.
Дата добавления: 2015-09-29; просмотров: 2535;
