Примеры решения задач. Задача 1. Смесь кислорода и азота при температуре t=270С находится под давлением Р=2,3·102 Па
Задача 1. Смесь кислорода и азота при температуре t=270С находится под давлением Р=2,3·102 Па. Масса кислорода составляет 75% от общей массы смеси. Определите концентрацию молекул каждого из газов.
| Дано: Т=300 К; Р=2,3·102 Па; m1=0,75 m; М1=0,032 кг/моль; М2=0,028 кг/моль. | Решение:
Смесь газов принимаем за идеальный газ, описываемый уравнением Менделеева– Клапейрона:
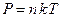 , (1)
где , (1)
где 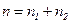 - (2) концентрация смеси газов; - (2) концентрация смеси газов; 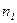 – концентрация молекул кислорода, – концентрация молекул кислорода, 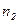 – концентрация молекул
азота; – концентрация молекул
азота; 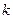 – постоянная Больцмана. – постоянная Больцмана.
|
| n1 - ? n2 - ? |
Из выражений (1) и (2) имеем:
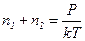 .
.  (3)
(3)
Выразим концентрацию n1 через концентрацию n2.
По условию задачи масса кислорода:
m1 = 0,75 m , (4)
где m – масса смеси.
Массу кислорода можно выразить также через концентрацию n1 и объем газа:
m1 = 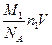 , (5)
, (5)
где М1 – молярная масса кислорода; NA – число Авогадро; V – объем газа.
Приравняв правые части выражений (4) и (5), получим:
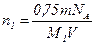 . (6)
. (6)
Масса азота m2=0,25m, или иначе 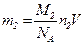 . Приравняв значения m2 из последних двух формул, найдем:
. Приравняв значения m2 из последних двух формул, найдем:
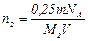 . (7)
. (7)
Из выражений (6) и (7) имеем:
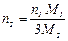 . (8)
. (8)
Подставив в формулу (3) значение n2 из последнего выражения, получим n1 = 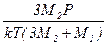 . После подстановки значений и вычисления n1 = 0,40·1023 1/м3, n2 = 0,15·1023 (1/м3).
. После подстановки значений и вычисления n1 = 0,40·1023 1/м3, n2 = 0,15·1023 (1/м3).
Ответ: n1 = 0,40·1023 1/м3, n2 = 0,15·1023 (1/м3).
Задача 2. В закрытом сосуде объемом V=1 м3 находится m1=1кг азота и m2=1,5 кг воды. Определите давление в сосуде при температуре t=6000С, зная, что при этой температуре вся вода превратится в пар.
| Дано: V=1 м3; m1=1 кг; m2=1,5 кг; Т=873 К; M1=0,028 кг/моль; M2=0,018 кг/моль. | Решение:
По закону Дальтона давление в сосуде после превращения воды в пар:
Р=Р1+Р2 , (1)
где Р1 - давление азота, Р2 – давление водяного пара. Состояние азота в сосуде определяется уравнением Менделеева - Клапейрона:
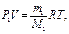 (2)
где M1 – молярная масса азота, R – универсальная газовая постоянная. Аналогично для водяного пара: (2)
где M1 – молярная масса азота, R – универсальная газовая постоянная. Аналогично для водяного пара:
 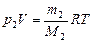 , (3)
где M2 – молярная масса водяного пара. , (3)
где M2 – молярная масса водяного пара.
|
| Р - ? |
Из уравнений (2) и (3) имеем: 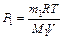 ,
, 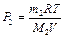 . После подстановки давлений Р1 и Р2 в выражение (1) имеем
. После подстановки давлений Р1 и Р2 в выражение (1) имеем 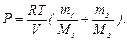 Используя числовые значения, получим: Р = 8,62·105 Па.
Используя числовые значения, получим: Р = 8,62·105 Па.
Ответ: Р = 8,62·105 Па.
Задача 3.Определите число молекул воздуха в аудитории объемом V=180 м3 при температуре t=220С и давлении Р=0,98·105 Па. Какова концентрация молекул воздуха при этих условиях?
| Дано: V=180 м3; Т=295 К; Р=0,98· 105 Па; | Решение:
Число молей воздуха в аудитории:
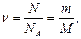 (1)
где – NA - число Авогадро, m – масса воздуха в аудитории, М – молярная масса воздуха.
Из выражения (1):
N = (1)
где – NA - число Авогадро, m – масса воздуха в аудитории, М – молярная масса воздуха.
Из выражения (1):
N = 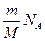 . (2) . (2)
|
| N - ? , n - ? |
Число молей воздуха в аудитории можно выразить, используя уравнение Клапейрона-Менделеева 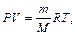 откуда
откуда 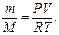 После подстановки
После подстановки 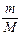 из последней формулы в выражение (2) получим:
из последней формулы в выражение (2) получим:
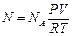 . (3)
. (3)
Используя числовые значения, определим N = 0,43·1028. Проверим единицы измерения правой части выражения (3) 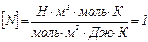 . Концентрацию (число молекул в единице объема) определим по формуле:
. Концентрацию (число молекул в единице объема) определим по формуле:
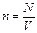 . После подстановки: n=0,24·1026
. После подстановки: n=0,24·1026 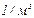 .
.
Ответ: N = 0,43·1028, n=0,24·1026 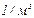 .
.
Задача 4.Определите среднюю квадратичную скорость молекул некоторого газа, плотность которого при давлении Р=1,1·105 Па равна ρ=0,024 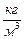 . Какова масса одного моля этого газа, если значение плотности дано для температуры 270 С?
. Какова масса одного моля этого газа, если значение плотности дано для температуры 270 С?
Дано:
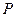 = 1,1·10 5 Па; = 1,1·10 5 Па;
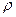 = 0,024 = 0,024 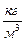 ; ;
 = 300 К. = 300 К.
| Решение:
Для определения средней квадратичной скорости движения молекул используем основное уравнение молекулярно-кинетической теории в таком виде:
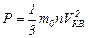 , (1)
где m0 – масса одной молекулы газа, n – концентрация молекул.
Так как m0n = ρ, то уравнение (1) можно записать , (1)
где m0 – масса одной молекулы газа, n – концентрация молекул.
Так как m0n = ρ, то уравнение (1) можно записать
|
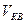 - ? - ? 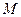 -? -?
|
в таком виде: 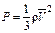 , откуда
, откуда 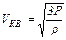 ,после подстановки числовых значений и вычисления получим:
,после подстановки числовых значений и вычисления получим:
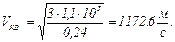
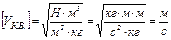 .
.
Для определения массы одного моля газа используем уравнение Клапейрона-Менделеева - 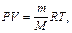 откуда
откуда 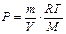 . Так как
. Так как 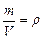 , то
, то 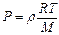 , или
, или 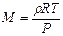 . После подстановки числовых значений и вычисления:
. После подстановки числовых значений и вычисления:
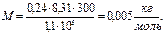
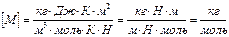 .
.
Ответ: 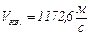 ,
, 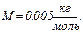
Дата добавления: 2015-09-28; просмотров: 3746;
