Примеры решения задач. Задача 1. Найдите момент инерции шара радиусом относительно оси , находящейся на расстоянии от поверхности шара (рис.3.1). Дано:
Задача 1. Найдите момент инерции шара радиусом 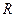 относительно оси
относительно оси 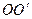 , находящейся на расстоянии
, находящейся на расстоянии 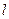 от поверхности шара (рис.3.1).
от поверхности шара (рис.3.1).
Дано:
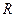 , ,  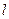
| Решение: Записываем теорему Штейнера: |
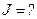
| 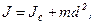 где где 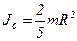 , ,
|
 - момент инерции шара относительно оси, проходящей через центр масс;
- момент инерции шара относительно оси, проходящей через центр масс; 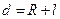 - расстояние между осями. Получаем:
- расстояние между осями. Получаем: 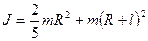 .
.
|
Задача 2.На шнуре, перекинутом через блок в виде однородного цилиндра массой 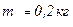 подвешены грузы массами
подвешены грузы массами 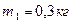 и
и 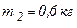 . Считаем нить невесомой и пренебрегаем трением в блоке. С каким ускорением движутся грузы? Каковы силы натяжения шнура, действующие на грузы во время движения?
. Считаем нить невесомой и пренебрегаем трением в блоке. С каким ускорением движутся грузы? Каковы силы натяжения шнура, действующие на грузы во время движения?
Дано: Решение:
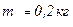 ; ;
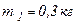 ; ;
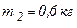 . .
| Делаем рисунок, расставляем силы, дейстующие на каждое тело и на блок (рис. 3.2):
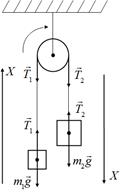 Рис.3.2
Рис.3.2
|
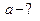 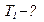 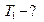
| |
Записываем второй закон Ньютона для каждого тела в векторной и скалярной форме:
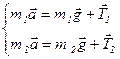
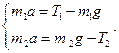 (1)
(1)
Для блока записываем основное уравнение динамики вращательного движения в векторной и скалярной форме:
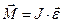
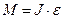 , (2)
, (2)
где 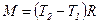 - момент сил,
- момент сил, 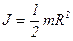 - момент инерции блока;
- момент инерции блока; 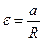 - угловое ускорение блока. Подставляя эти выражения в (2), получаем:
- угловое ускорение блока. Подставляя эти выражения в (2), получаем:
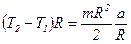 , т.е.
, т.е. 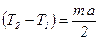 . (3)
. (3)
Решая совместно уравнения (1) и (3), получаем:
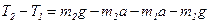 . Отсюда:
. Отсюда:
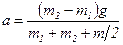 ,
,
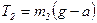 ,
, 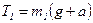 .
.
Подставляем числа: 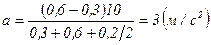 ,
,
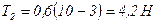 ,
,
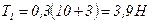 .
.
Ответ: 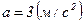 ,
, 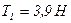 ,
, 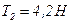 .
.
Задача 3. Шар и обруч одинаковой массы и радиуса, изготовленные из одного и того же материала, катятся без скольжения с одинаковой скоростью. Во сколько раз кинетическая энергия шара меньше кинетической энергии обруча?
Дано: Решение:
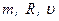
| Кинетическая энергия тела, катящегося по поверхности, складывается из кинетической энергии вращательного движения и поступательного движения центра масс: |
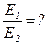
|
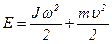 . (1)
. (1)
Моменты инерции относительно центра масс обруча 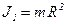 (2) и шара
(2) и шара 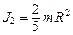 (3). Связь линейной и угловой скорости -
(3). Связь линейной и угловой скорости - 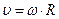 (4). Подставляя (2), (3) и (4) в (1), получаем:
(4). Подставляя (2), (3) и (4) в (1), получаем:
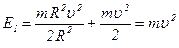 - для обруча,
- для обруча,
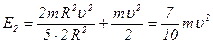 - для шара.
- для шара.
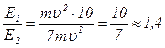
Ответ: в 1,4 раза.
Дата добавления: 2015-09-28; просмотров: 4811;
